
题目列表(包括答案和解析)
3.g(x)=1-2x,f[g(x)]=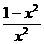 (x≠0),则f(
(x≠0),则f(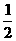 )等于( )
)等于( )
A.1 B.3 C.15 D.30
答案:C
解析:令g(x)=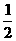 ,则x=
,则x=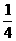 ,
,
∴f(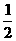 )=
)=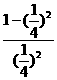 =15.
=15.
2.若f(x+1)=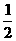 f(x),则下列函数中f(x)为( )
f(x),则下列函数中f(x)为( )
A.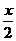 B.x+
B.x+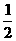 C.2-x
D.
C.2-x
D.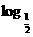 x
x
答案:C
解析:当f(x)=2-x时,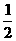 f(x)=2-x-1,f(x+1)=2-(x+1),故选C.
f(x)=2-x-1,f(x+1)=2-(x+1),故选C.
1.(2010江苏南京一模,2)函数y=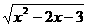 +log2(x+2)的定义域为( )
+log2(x+2)的定义域为( )
A.(-∞,-1)∪(3,+∞) B.(-∞,-1]∪[3,+∞)
C.(-2,-1] D.(-2,-1]∪[3,+∞)
答案:D
解析: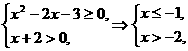 或x≥3
或x≥3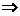 -2<x≤-1或x≥3.
-2<x≤-1或x≥3.
14.已知函数f(x)=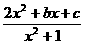 (b<0)的值域为[1,3].
(b<0)的值域为[1,3].
(1)求实数b、c的值;
(2)判断F(x)=lgf(x)在x∈[-1,1]上的单调性,并给出证明.
解析:(1)由y=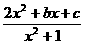 ,知x∈R,去分母,整理得(2-y)x2+bx+c-y=0,(*)
,知x∈R,去分母,整理得(2-y)x2+bx+c-y=0,(*)
当y-2≠0时,由x∈R有Δ=b2-4(2-y)(c-y)≥0,
即4y2-4(2+c)y+8c-b2≤0,由题设及二次不等式与方程的关系得2+c=1+3且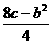 =1×3,解之得b=±2,c=2,又b<0,
=1×3,解之得b=±2,c=2,又b<0,
∴b=-2,c=2.
当y-2=0时,将b=-2,c=2代入(*)式得x=0,适合
∴b=-2,c=2为所求.
(2)F(x)在x∈[-1,1]上是减函数.
证明:设-1≤x1<x2≤1,
则F(x2)-F(x1)=lg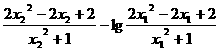
=lg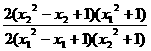
=lg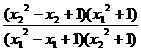 .
.
而(x22-x2+1)(x12+1)-(x12-x1+1)(x22+1)
=x1x2(x2-x1)-(x2-x1)
=(x2-x1)(x1x2-1),
又∵x2>x1,∴x2-x1>0.
又|x1|≤1,|x2|≤1,由x1≠x2,
∴|x1||x2|≤1.
∴-1≤x1x2<1,∴x1x2-1<0.
∴0<(x22-x2+1)(x12+1)<(x12-x1+1)(x22+1).
∴0<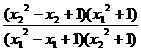 <1.
<1.
∴F(x2)-F(x1)
=lg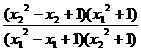 <0.
<0.
即F(x2)<F(x1),
故F(x)=lgf(x)在[-1,1]上是减函数.
13.已知函数f(x)=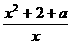 ,x∈[1,+∞).
,x∈[1,+∞).
(1)当a=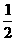 时,求函数f(x)的最小值;
时,求函数f(x)的最小值;
(2)若对任意x∈[1,+∞],f(x)>0恒成立,试求实数a的取值范围.
解析:(1)当a=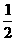 时,f(x)=
时,f(x)=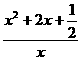 =x+
=x+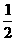 x+2,
x+2,
易证f(x)在[1,+∞)单调递增,
∴f(x)min=f(1)=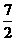 .
.
(2)x∈[1,+∞),f(x)>0恒成立,即t=x2+2x+a在[1,+∞)恒大于0.
而t在[1,+∞)递增,∴tmin=2+a.
依题意知2+a>0,∴a>-2为所求.
12.若函数y=f(x)=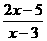 的值域是[-4,2],求f(x)的定义域.
的值域是[-4,2],求f(x)的定义域.
解析:由y=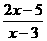 及-4≤y<2得-4≤
及-4≤y<2得-4≤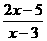 <2,解得x≤
<2,解得x≤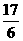 .
.
11.已知函数f(x)的值域为[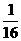 ,16],求函数?g(x)=f(x)+2
,16],求函数?g(x)=f(x)+2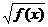 及h(x)=f(x)-2
及h(x)=f(x)-2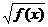 的值域.
的值域.
解析:令t=f(x),则g(x)=G(t)=t+2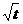 ,G(t)在[
,G(t)在[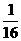 ,16]上为增函数,值域为[
,16]上为增函数,值域为[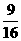 ,24].
,24].
h(x)=H(t)=t-2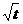 =(
=(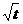 -1)2-1∈[-1,8].
-1)2-1∈[-1,8].
10.函数y=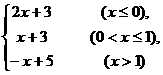 的值域为________________.
的值域为________________.
答案:(-∞,4]
解析:当x≤0时,y=2x+3∈(-∞,3];
当0<x≤1时,y=x+3∈(3,4];
当x>1时,y=-x+5∈(-∞,4].
∴函数的值域为(-∞,3]∪(3,4]∪(-∞,4)=(-∞,4].
9.函数y=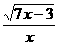 在[
在[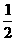 ,3]上的最小值是________________.
,3]上的最小值是________________.
答案: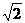
解析:y=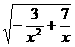
=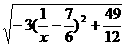 ,令t=
,令t=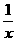 ,
,
则y=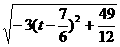 ,t∈[
,t∈[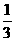 ,2],当t=
,2],当t=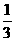 或2时,y取最小值
或2时,y取最小值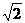 .
.
8.函数f(x)=log2(32-x2)的定义域为A,值域为B,则A∩B=_____________.
答案:[-4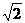 ,5]
,5]
解析:由32-x2>0知-4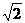 <x<4
<x<4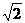 ,∴A=[-4
,∴A=[-4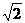 ,4
,4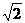 ].
].
又∵32-x2∈(0,32),
∴B=(-∞,5),A∩B=[-4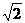 ,5].
,5].
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com