
题目列表(包括答案和解析)
11.是否存在实数a,使得函数f(x)=log2(x+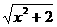 )-a为奇函数,同时使函数g(x)= x(
)-a为奇函数,同时使函数g(x)= x(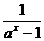 +a)为偶函数?证明你的结论.
+a)为偶函数?证明你的结论.
证明:若f(x)是奇函数,则f(x)+f(-x)=0,即
log2(x+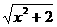 )+log2(-x+
)+log2(-x+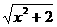 )-2a=0.
)-2a=0.
整理得log2(x2+2-x2)-2a=0,∴a=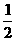 .
.
若g(x)为偶函数,则g(x)-g(-x)=0,即
x(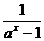 +a)+x(
+a)+x(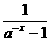 +a)=0.
+a)=0.
化简,得x(-1+2a)=0,∴a=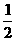 .
.
综上,存在a=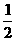 满足条件.
满足条件.
10.试构造一个函数f(x),x∈D,使得对一切x∈D有|f(-x)|=|f(x)|恒成立,但是f(x)既不是奇函数又不是偶函数,则f(x)可以是______________.
答案:f(x)=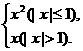 (答案不唯一)
(答案不唯一)
解析:f(x)的图象部分关于原点对称,部分关于y轴对称,故可以用分段函数来构造.
9.若φ(x)与g(x)都是奇函数,且f(x)=aφ(x)+bg(x)+2在(0,+∞)上有最大值5,则f(x)在(-∞,0)上有最____________值,该值等于______________.
答案:小 -1
解析:设h(x)=f(x)-2,
∴h(x)=aφ(x)+bg(x),
∵φ(x)与g(x)都是奇函数,
∴h(x)是奇函数,由题可知h(x)在(0,+∞)上的最大值为3;故h(x)在(-∞,0)上有最小值,该值为-3,即f(x)-2在(-∞,0)上有最小值为-3,∴f(x)的最小值为-1.
8.(2010全国大联考,14)已知f(x)为偶函数,g(x)是奇函数,且f(x)-g(x)=x2+x-2,则f(x),g(x)分别为___________________.
答案:x2-2,-x
解析:∵f(x)-g(x)=x2+x-2,∴f(x)+g(x)=x2-x-2,故f(x)=x2-2,g(x)=-x.
7.设函数f(x)(x∈R)为奇函数,f(1)=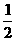 ,f(x+2)=f(x)+f(2),则f(5)等于( )
,f(x+2)=f(x)+f(2),则f(5)等于( )
A.0
B.1
C.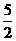 D.5
D.5
答案:C
解析:令x=-1,则f(1)=f(-1)+f(2),即f(2)=2f(1)=1;令x=3,则f(5)=f(3)+f(2)=[f(1)+f(2)]+f(2)=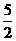 .
.
6.已知f(x)是R上的偶函数,且在[0,+∞)上是减函数,f(a)=0(a>0),那么不等式xf(x)<0的解集是( )
A.{x|0<x<a} B.{x|-a<x<0或x>a}
C.{x|-a<x<a} D.{x|x<-a或0<x<a}
答案:B
解析:利用图象法,画出符合条件的函数图象,如下图,由此可知,选项B正确.
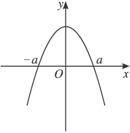
5.已知f(x)是周期为2的偶函数,且在区间[0,1]是增函数,则f(-6.5),f(-1),f(0)的大小关系为( )
A.f(-6.5)<f(0)<f(-1) B.f(-1)<f(-6.5)<f(0)
C.f(0)<f(-6.5)<f(-1) D.f(-1)<f(0)<f(-6.5)
答案:C
解析:f(-6.5)=f(-3×2-0.5)=f(-0.5)=f(0.5),f(-1)=f(1).
∵f(x)在[0,1]单调递增,∴f(0)<f(0.5)<f(1)即f(0)<f(-6.5)<f(-1).
4.(2010湖北八校模拟,6)设函数f(x)是定义在R上,周期为3的奇函数,若f(1)<1,?f(2)=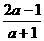 ,则( )
,则( )
A.a<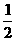 且a≠-1
B.-1<a<0
且a≠-1
B.-1<a<0
C.a<-1或a>0 D.-1<a<2
答案:C
解析:由题意得,f(-2)=f(1-3)=f(1)<1,
∴-f(2)<1.即-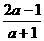 <1.∴
<1.∴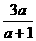 >0,即3a(a+1)>0.∴a<-1或a>0.故选C.
>0,即3a(a+1)>0.∴a<-1或a>0.故选C.
3.若a>0,a≠1,f(x)为偶函数,则g(x)=f(x)·loga(x+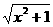 )的图象( )
)的图象( )
A.关于x轴对称 B.关于y轴对称
C.关于原点对称 D.关于直线y=x对称
答案:C
解析:∵g(-x)=f(-x)·loga(-x+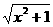 )=f(x)·loga(x+
)=f(x)·loga(x+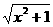 )-1=-f(x)·loga(x+
)-1=-f(x)·loga(x+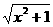 )=-g(x),
)=-g(x),
∴g(x)为奇函数.
2.已知f(x)=a-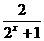 是奇函数,那么实数a的值等于( )
是奇函数,那么实数a的值等于( )
A.1 B.-1 C.0 D.±1
答案:A
解析:f(x)为奇函数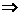 f(0)=0
f(0)=0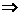 a-
a-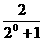 =0
=0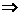 a=1.
a=1.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com