
题目列表(包括答案和解析)
例3已知三条直线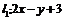 ,
,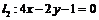 ,
,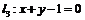 ,能否找到一点
,能否找到一点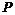 ,使得
,使得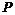 点同时满足下列三个条件:①
点同时满足下列三个条件:①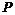 是第一象限的点;②
是第一象限的点;②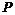 点到
点到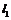 的距离是
的距离是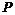 点到
点到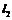 的距离的
的距离的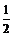 ;③
;③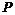 点到
点到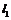 的距离与
的距离与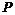 点到
点到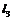 的距离之比是
的距离之比是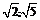 .若能,求出
.若能,求出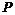 点坐标;若不能,说明理由.
点坐标;若不能,说明理由.
分析:求解本题所必需的工具是两个公式:平行直线间的距离公式及点到直线的距离公式.然后再根据①,②,③建立起来的方程组求解.
解:设存在点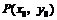 ,且点
,且点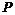 在
在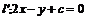 上,
上,
由点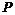 满足条件②,得
满足条件②,得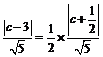 ,
,
解得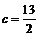 或
或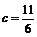 .
.
 或
或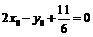 .
.
由点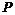 满足条件③,得
满足条件③,得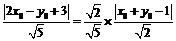 ,
,
即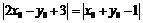 .
.
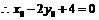 或
或 不可能,
不可能,
联立方程组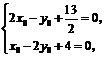 解得
解得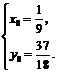
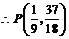 即为所求.
即为所求.
例4 设动点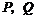 的坐标分别为
的坐标分别为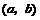 和
和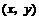 ,且满足
,且满足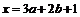 ,
, ,如果点
,如果点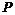 在直线
在直线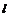 上移动,点
上移动,点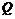 也在直线
也在直线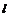 上移动,这样的直线
上移动,这样的直线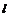 是否存在?若存在,求出直线
是否存在?若存在,求出直线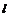 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
分析:“点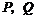 在直线
在直线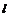 上移动”可以理解为直线既是由点
上移动”可以理解为直线既是由点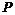 运动而成的,又是由点
运动而成的,又是由点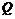 运动而成的,即直线
运动而成的,即直线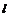 是经过
是经过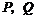 两点的直线.这样,先设出直线
两点的直线.这样,先设出直线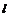 的方程,借助坐标变换,再由两直线重合的条件利用待定系数法求解.
的方程,借助坐标变换,再由两直线重合的条件利用待定系数法求解.
解:假设存在这样的直线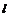 ,设其方程为
,设其方程为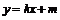 ,
,
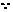 点
点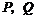 都在
都在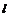 上移动,于是有
上移动,于是有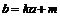 ,
,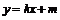 .
.
又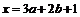 ,
, ,
,
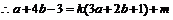 ,即
,即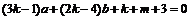 .
.
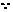 此直线与直线
此直线与直线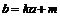 重合,则有
重合,则有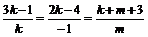 ,
,
解得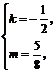 或
或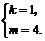
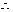 直线
直线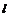 的方程为
的方程为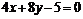 或
或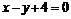 .
.
点评:上述两题都属于“存在型探索题”.解这类问题的一般方法是假设存在,利用相关知识加以推理.若推出矛盾,则假设不成立;否则,假设的命题成立.
例1 将一张坐标纸折叠一次,使得点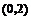 与点
与点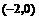 重合,且点
重合,且点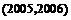 与点
与点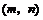 重合,则
重合,则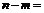 .
.
解析: 折叠之后点
折叠之后点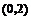 与点
与点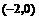 重合,
重合,
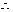 两点关于直线
两点关于直线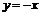 对称.
对称.
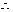 点
点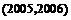 关于直线
关于直线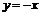 的对称点为
的对称点为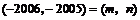 .
.
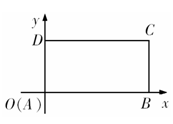
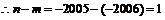 .
.
例2 在平面直角坐标系中,已知矩形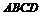 的长为2,宽为1,
的长为2,宽为1,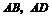 边分别在
边分别在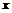 轴,
轴,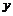 轴的正半轴上,
轴的正半轴上,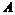 点与坐标原点重合(如图所示).将矩形折叠,使
点与坐标原点重合(如图所示).将矩形折叠,使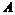 点落在线段
点落在线段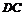 上.若折痕所在直线的斜率为
上.若折痕所在直线的斜率为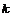 ,试写出折痕所在直线的方程.
,试写出折痕所在直线的方程.
解:①当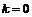 时,
时,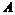 点与
点与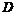 点重合,折痕所在的直线方程为
点重合,折痕所在的直线方程为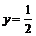 ;
;
②当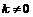 时,设将矩形折叠后
时,设将矩形折叠后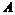 落在线段
落在线段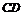 上的点为
上的点为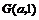 ,
,
所以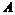 与
与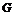 关于折痕所在的直线对称,故有
关于折痕所在的直线对称,故有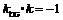 ,解得
,解得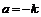 .
.
故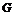 点坐标为
点坐标为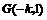 .
.
从而折痕所在的直线与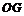 的交点坐标(线段
的交点坐标(线段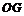 的中点)为
的中点)为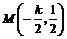 .
.
所以折痕所在的直线方程为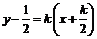 ,即
,即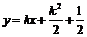 .
.
由①,②得折痕所在的直线方程为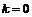 时,
时,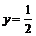 ;
;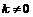 时,
时,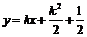 .
.
点评:上述两题以“折叠”为载体,考查了直线方程关于直线对称或者是点对称等知识,是一类情景新颖的活题,给直线方程问题又增添了“动”的活力.
例5 已知实数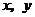 满足
满足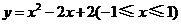 ,试求
,试求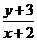 的最大值和最小值.
的最大值和最小值.
分析:利用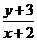 的几何意义:连结定点
的几何意义:连结定点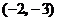 与动点
与动点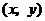 的直线的斜率,借助数形结合,将求最值问题转化为求斜率取值范围问题,简化运算过程.
的直线的斜率,借助数形结合,将求最值问题转化为求斜率取值范围问题,简化运算过程.
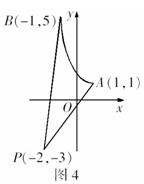 解:如图4,由
解:如图4,由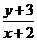 的几何意义可知,它表示经过定点
的几何意义可知,它表示经过定点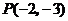 与曲线段
与曲线段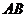 上任一点
上任一点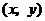 的直线的斜率
的直线的斜率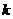 .
.
易知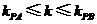 ,
,
由已知,可得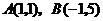 .
.
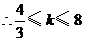 ,
,
故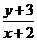 的最大值是8,最小值是
的最大值是8,最小值是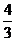 .
.
评注:巧妙利用斜率公式,借助数形结合直观求解,收到事半功倍的效果,此题还可利用后边所学内容,用代数的方法求解.
例4
如果三点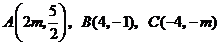 在同一条直线上,试确定常数
在同一条直线上,试确定常数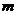 的值.
的值.
分析:如果三点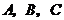 在同一条直线上,则直线
在同一条直线上,则直线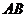 的斜率与直线
的斜率与直线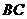 的斜率相等.
的斜率相等.
解:由于三点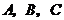 所在直线不可能垂直于
所在直线不可能垂直于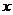 轴,
轴,
因此设直线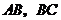 的斜率分别为
的斜率分别为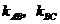 .
.
由斜率公式,得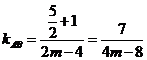 ,
,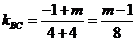 .
.
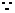
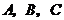 在同一条直线上,
在同一条直线上,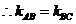 .
.
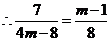 ,即
,即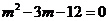 .
.
解得 ,或
,或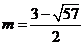 .
.
评注:两直线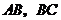 的斜率相等,则
的斜率相等,则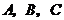 三点共线;反过来,若
三点共线;反过来,若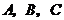 三点共线,则直线
三点共线,则直线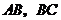 的斜率相等(斜率存在时),或都不存在.
的斜率相等(斜率存在时),或都不存在.
例3 已知函数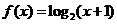 ,且
,且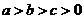 ,则
,则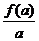 ,
,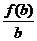 ,
,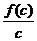 的大小关系为( )
的大小关系为( )
A.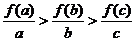 B.
B.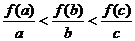
C. D.
D.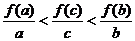
分析:该题从特殊值和常规方法都不容易找到解题的捷径,经仔细分析发现,其结构具务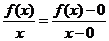 的特点,由此联想到利用斜率进行求解.
的特点,由此联想到利用斜率进行求解.
 解:作出函数
解:作出函数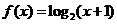 的大致图象(图3).
的大致图象(图3).
由图(3)可知,曲线上各点与原点连线的斜率随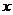 的增大而减小.因为
的增大而减小.因为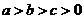 ,所以
,所以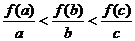 .故选(B).
.故选(B).
例2 已知线段的两个端点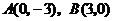 ,若直线
,若直线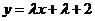 与线段
与线段 相交,求实数
相交,求实数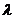 的取值范围.
的取值范围.
分析:采用数形结合的方法,因为直线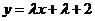 恒过一个定点,并且斜率为
恒过一个定点,并且斜率为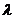 ,则直线应落在定点与
,则直线应落在定点与 的连线之间,从而得出斜率所取的范围,即可确定
的连线之间,从而得出斜率所取的范围,即可确定 的取值范围.
的取值范围.
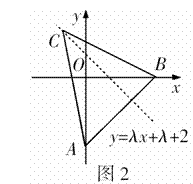 解:如图2,
解:如图2,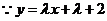 恒经过一定点
恒经过一定点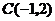 ,
,
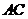 的斜率
的斜率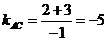 ,
,
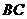 的斜率
的斜率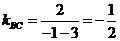 .
.
若直线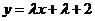 与线段
与线段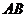 相交,
相交,
则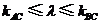 .
.
故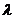 的取值范围是
的取值范围是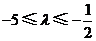 .
.
评注:数形结合是求直线与直线及直线与平面曲线位置关系问题的好方法,它直观简明,计算量小,是解答小题的首选方法,也是解答大题的重要方法.
例1
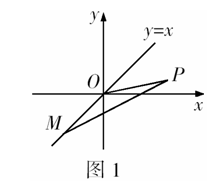
已知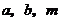 均为正数,且
均为正数,且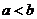 ,求证:
,求证: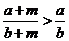 .
.
分析:观察所证不等式的左边,结构与斜率公式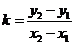 很相似,
很相似, ,
,
显然此式可看作点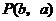 与点
与点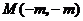 的连线的斜率.
的连线的斜率.
解:如图1,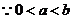 ,
,
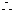 点
点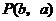 在第一象限,
在第一象限,
且必位于直线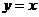 的下方.
的下方.
又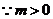 ,
,
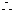 点
点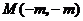 在第三象限,且必在
在第三象限,且必在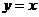 上.
上.
连结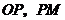 ,则
,则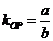 ,
,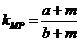 .
.
 直线
直线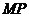 的倾斜角大于直线
的倾斜角大于直线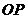 的倾斜角,
的倾斜角,
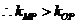 ,即有
,即有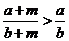 .
.
由于两个独立条件确定一条直线,因此,在求直线方程时,可根据直线系概念,先写出满足其中一个条件的直线系方程,然后用另一个条件求出直线系方程中的参数,即得我们所要求解的直线方程。平常实际教学中,直线系方程第一、第二和第三种常见类型我们用的比较多,而直线系方程第四种常见类型也有很好的用处。下面主要阐述直线系方程第四种常见类型的应用。
例1、已知三角形三边所在的直线方程分别为: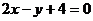 ,
,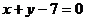 ,
,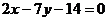 ,求边
,求边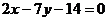 上的高所在的直线方程。
上的高所在的直线方程。
分析:此题解题方法比较多,常规方法计算较多,若引入直线系方程,则运算简便,解法精彩。
解析:设所求高所在的直线方程为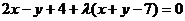 ,
,
即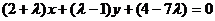 ,
,
则由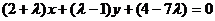 与
与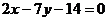 垂直,
垂直,
可得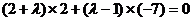 ,解得
,解得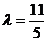 ,
,
所以所求高所在的直线方程为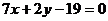 。
。
例2、求过直线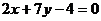 与
与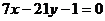 的交点,且和
的交点,且和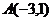 、
、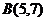 等距离的直线方程。
等距离的直线方程。
分析:此题解题常规方法为设点斜式直线方程,但这样默认了所求直线的斜率存在的情况,往往遗漏了斜率不存在时的直线方程。若引入对应的直线系方程,则避免了这种情况的发生,解法非常巧妙。
解析:设所求直线方程为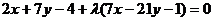 ,
,
即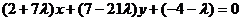 ,
,
由点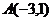 、
、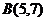 到所求直线等距离,可得
到所求直线等距离,可得
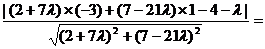
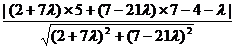 ,
,
整理可得 ,
,
解得 或
或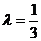 ,
,
所以所求高所在的直线方程为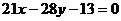 或
或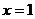 。
。
4、过两条已知直线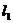 :
: 和
和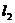 :
: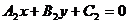 的交点的直线系方程是:
的交点的直线系方程是: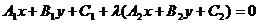 (
(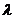 是参数,当
是参数,当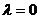 时,方程变为
时,方程变为 ,恰好表示直线
,恰好表示直线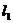 ;当
;当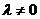 时,方程表示过直线
时,方程表示过直线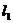 和
和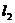 的交点,但不含直线
的交点,但不含直线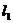 和
和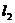 的任一条直线)。
的任一条直线)。
3、垂直于已经直线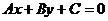 的直线系方程是:
的直线系方程是: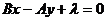 (
(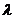 是参数);
是参数);
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com