1、已知△ABC中，∠B是锐角，从顶点A向边BC或它的边延长线引垂线交BC 于H 点，又从顶点C 向边AB或它的延长线引垂线，交AB 于K点，试问：当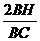　 和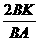均为整数时，△ABC是怎样的三角形？并证明你的结论。

6、(1)试设计一种方法，把一个正方形不重复不遗漏的地分割成8个正方形(分得的正方形大小可以不相同)；又问如何把正方形按上述要求分成31个正方形。

(2)试设计一种方法，把一个立方体分割成55个立方体(分得的立方体大小可以不相同)。

5、用24个面积为1的单位正三角表拼成如图所示的正六

边形，我们把面积为4的正三角形称为“希望形”。

(1)请你回答，图中共可数出多少个不同的“希望形”？

(2)将1-24这二十四个自然数填入二十四个单位正三角

形中(每个里只填一个数)。我们依次对所有“希望形”中的四

个单位正三角形中填的数同时加上一个相同的自然数称为一次操作，问能否经过有限次操作后，使图中二十四个单位正三角形中都变为相同的自然数？如果能，请给出一种填法，如果不能，请简述理由。

4、(a)请你在平面上画出6条直线(没有三条共点)，使得它们中的每条直线都恰与另三条直线相交，并简单说明画法。

(b)能否在平面上画出7条直线(任意三条都不共点)，使得它们中的每条直线都恰与另三条直线相交？如果能请画出一例，如果不能请简述理由。

3、平面上给定四个点，两两连结这四点的诸直线不平行，不垂直，也不重合。过每一点作其余三点两两连结的直线的垂线，若不算已知的四点，这些垂线间有多少个不同交点？证明你的结论。

2、(1)用1×1，2×2，3×3三种型号的正方形地板砖铺设23×23的正方形地面，请你设计一种铺设方案，使得1×1的地板砖只用一块。

(2)请你证明：只用2×2，3×3两种型号的地板砖，无论如何铺设都不能铺满23×23的正方形地面而不留空隙。

1、从1，2，……，16中，最多能选出多少个数，使得被选出的数中，任意三个数都不是两两互质。

6、从数1，2，3，……，1995中任意取出n个不同的数(1≤n≤1995)形成一组叫做一个n元数组，如(1，2，3，4)就是一个四元数组，(4，8，12，20，32)就是一个五元数组。现要给出一个自然数k，使得每一个k元数组中总能找到三个不同的数，此三数能构成一个三角形的三边长，则给出的k至少是多少时才能满足要求？证明你的结论。

5、在一次有n个足球队参加的循环赛中(即每一队必须同其余各个队进行一场比赛)，每场比赛胜队积2分，平局各积1分，败队积0分，结果有一队积分比其他各队都多，而胜的场次比其他任何一队都少，求n最小的可能值。

4、平面上给定了2n个点，其中任意三点不共线，并且n个点染成了红色，n个点染成了蓝色，证明：总可以找到两两没有公共点的n条直线段，使得其中每条线段的两个端点具有不同的颜色。