
题目列表(包括答案和解析)
1、某弦将圆分成1:4两部分,则劣弧的度数为_____度,劣弧所对的圆周角为______度。
6. 汽车路线由周长10英里的环路和从总站到环路上Q点长1英里的直线组成(如图),两部汽车在路上服务,每部周游需要20分,1号车离开总站,沿着直路走,按顺时针方向绕环路一次,又沿直线回到总站,2号车到达总站比1号车迟到10分,走同样的路线,但按返时针方向绕行环路。两部车连续行驶,在路上的任何地点都不耽搁,只有让乘客上、下车的时间可以忽略。
一个人打算在地点P候车,那里沿1号车路线离开总站x英里(0≤x<12=要搭车到总站去,假定他搭上使他尽早达到目的地的汽车,他的旅行所需的最长的时间为W(x) (候车时间加乘车时间).
求W(2),W(4).
对于x的什么值, 时间W(x)最长?
对0≤x<12画出y = W(x)的草图.
5. 观察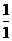 =
=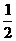 +
+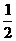 ;
;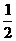 =
=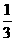 +
+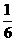 ;
;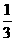 =
=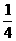 +
+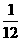 ;
;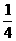 =
=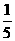 +
+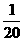 。由这些例子的启发,叙述一般规律,并加以证明。对任何大于1的整数n,证明存在正整数i和j,使得
。由这些例子的启发,叙述一般规律,并加以证明。对任何大于1的整数n,证明存在正整数i和j,使得
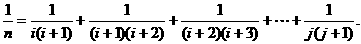
4. 一个四边形在边长为1的正方形各边上各有一点,证明四边形的边长a,b,c,d满足不等式2≤a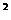 +b
+b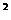 +c
+c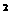 +d
+d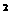 ≤4.
≤4.
3. 求证:不存在这样的整数,把它的首位数字移到末位之后,得到的数是原数的两倍.
2. 设a , b ,p , q
, r , s为正整数,满足qr-ps=1, 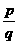 <
<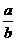 <
<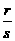 。证明:b≥q+s。
。证明:b≥q+s。
1. 解方程组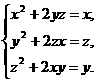
6、平面上已给7个点,用一些线段连接它们,使得(1)每三点中至少有两点相连;(2)线段的条数最少。问有多少条线段?给出一个这样的图。
5、平面上有40个点,任何三点不共线,已知每一点至少和其余27个点之间有线段连接。求证:必可找到4个点A,B,C,D,它们之中任何两点间都有线段连接。
4、有27个国家参加的一次国际会议,每个国家有两名代表,求证:不可能将54名代表安排在一张圆桌的周围就坐,使得任一国的两位代表之间都夹有9个人。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com