7.某商店出售一种瓜子，其售价y(元)与瓜子质量x(千克)之间的关系如下表

由上表得y与x之间的关系式是 　　　　　　　　　　　.

8在计算器上按照下面的程序进行操作：

下表中的x与y分别是输入的6个数及相应的计算结果：

上面操作程序中所按的第三个键和第四个键　　

应是　　　　　　　　 .　　

6.写出同时具备下列两个条件的一次函数表达式(写出一个即可)　　　 　　　　　.

(1)y随着x的增大而减小。　　 (2)图象经过点(1，-3)

5．　 某种储蓄的月利率为0.15%，现存入1000元，则本息和y(元)与所存月数x之间的函数关系式是　　　　　　　　　　　 .

4．　 下列三个函数y= -2x,　 y= - x,　 y=(- )x共同点是(1)　　　　　　　 ;

(2)　　　　　　　　　　　 ;(3)　　　　　　　　　　 .

3．　 一次函数y= -2x+4的图象与x轴交点坐标是　　　　 ，与y轴交点坐标是　　　　 　

　图象与坐标轴所围成的三角形面积是 　　　　　.

2．　 已知一次函数y=kx+5的图象经过点(-1，2)，则k= 　　　　　.

1．　 已知一个正比例函数的图象经过点(-2，4)，则这个正比例函数的表达式是　　　 .　

2、已知某一次函数的图象经过点(0, -3),且与正比例函数y= x的图象相交于

点(2，a),求　　 (1)　 a的值。

(2)　　 k、b的值。

(3)　　 在同一直角坐标系中画出这两个函数的图象。

(4)　　 这两个函数图象与x轴所围成的三角形面积。　

1、如图的折线表示一辆自行车离家的距离与时间的关系，骑车者9：00离开家，15：00回家，根据图象回答：

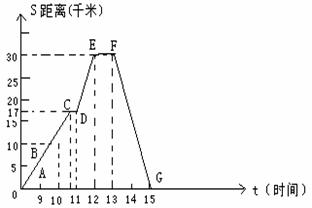(1)离家最远的距离是　　　千米，对应的时间是　　　　.

(2)何时开始第一次休息？答：　　　　　 ， 休息多长时间？答：　　　　　　　

(3)第一次休息时，离家多远？答：　　　　　　　　　　　　　

(4)在11：00－12：00他骑车的路程是多少千米？答：　　　　　　　　　　　

(5)在9：00－10：00和10：00－10：30的平均速度各是多少？答：　　　　　　

(6)他在何时至何时停止前进并休息午餐？

答：　　　　　　　　　　

(7)他在停止前进后返回，骑了多少千米？

答：　　　　　　　　　　　

(8)返回时的平均速度是多少？

答：　　　　　　　　　　　

(9)11：30和13：30分别离家多远？答：　　　　　　　　　　　　

(10)何时距家22千米？答：　　　　　　　　　　　　　　　　　　

6.如图，已知A地在B地正南方3千米处，甲乙两人同时分　　 别从A、B两地向正北方向匀速直行，他们与A地的距离S(千米)与所行的时间t(小时)之间的函数关系图象如图所示的AC和BD给出，当他们行走3小时后，他们之间的距离为　　　　 千米.