
题目列表(包括答案和解析)
7.若函数y=(m+2)x|m|-3是反比例函数,则m的值是( )
A.2 B.-2 C.±2 D.以上答案均不正确
6.在第三象限中,下列函数,y随x的增大而减小的有( )。
①、y=-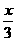 ②、y=
②、y= ③、y=-2x+5 ④、y=-5x-6
③、y=-2x+5 ④、y=-5x-6
A.1个 B.2个 C.3个 D.4个
5.若点(3,4)是反比例函数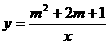 图象上一点,则此函数图象
必经过点(
)
图象上一点,则此函数图象
必经过点(
)
A.(3,-4) B.(2,-6) C.(4,-3) D. (2,6)
4.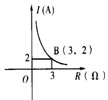 某闭合电路中,电源电压为定值,电流I(A)与电阻R(Ω)成反比例,如右图所表示的是该电路中电流I与电阻R之间的函数关系的图象,则用电阻R表示电流I的函数解析式为( ).
某闭合电路中,电源电压为定值,电流I(A)与电阻R(Ω)成反比例,如右图所表示的是该电路中电流I与电阻R之间的函数关系的图象,则用电阻R表示电流I的函数解析式为( ).
A.I=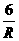 B.I=-
B.I=-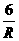 C.I=
C.I= D.I=
D.I=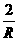
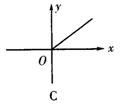
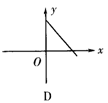
3.已知矩形的面积为10,则它的长y与宽x之间的关系用图象表示大致为( )
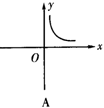
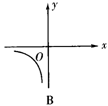
2.反比例函数y=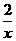 的图象位于( )
的图象位于( )
A.第一、二象限 B.第一、三象限 C.第二、三象限 D.第二、四象限
1.下列函数中,y是x的反比例函数的为( )
A.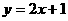 B.
B.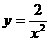 C.
C.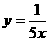 D.
D.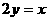
1.二次根式的概念
定义:
式子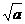
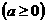 叫做二次根式,其中注意 在实数范围内,a< 0时,
叫做二次根式,其中注意 在实数范围内,a< 0时,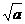 没有意义,只有当a≥0时,
没有意义,只有当a≥0时,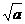 有意义。a叫做被开方式。
有意义。a叫做被开方式。
例1 : 判断,下列各式中那些是二次根式?
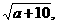
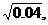
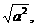
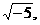
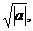
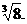
定义:式子 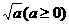 叫做二次根式. 其中a叫做被开方式。
叫做二次根式. 其中a叫做被开方式。
例 2 x是怎样的实数时,式子 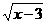 在实数范围内有意义?
在实数范围内有意义?
解 由 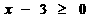 ,得
,得 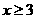 。
。
当 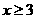 时,式子
时,式子 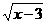 在实数范围内有意义。
在实数范围内有意义。
试一试(2) x是怎样的实数时,下列各式在实数范围内有意义?
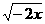
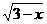
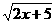
二次根式的性质(1)
想一想 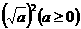 等于什么?请举例验证.
等于什么?请举例验证.
试一试(3)计算:
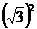
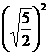
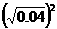
利用这个式子,我们可以把任何一个非负数写成一个数的平方的形式。
试一试(4)把下列各数写成平方的形式:
3= 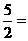
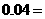
1.二次根式的概念
想一想:
、平方根的性质:
正数有两个平方根且互为相反数;
0有一个平方根就是它0;
负数没有平方根。
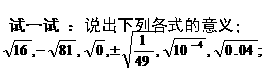
上面几个式子中,被开方数的特点?
被开方数是非负数
16.2 二次根式
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com