
题目列表(包括答案和解析)
5、两直线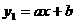 与
与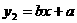 在同一坐标系内的图象可能是 ( )
在同一坐标系内的图象可能是 ( )

A B C D
4、下列图中,不表示某一函数图象的是 ( )

A B C D
3、直线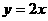 ,
,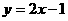 ,
,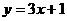 共同具有的特征是 ( )
共同具有的特征是 ( )
A.经过原点
B.与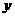 轴交于负半轴 C.
轴交于负半轴 C.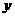 随
随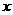 增大而增大 D.
增大而增大 D.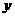 随
随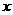 增大而减小
增大而减小
2、函数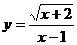 中自变量
中自变量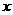 的取值范围是 ( )
的取值范围是 ( )
A.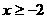 B.
B.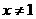 C.
C.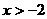 且
且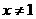 D.
D.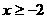 且
且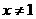
1、下列函数 (1)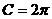
 (2)
(2)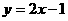 (3)
(3)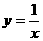 (4)
(4)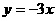 (5)
(5)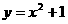 中,是一次函数的有(
) A.4个 B.3个 C.2个 D.1个
中,是一次函数的有(
) A.4个 B.3个 C.2个 D.1个
3.解析:(1)设L1的解析式为y1=k1x+2,由图像得17=500k1+2,解得k=0.03,
∴y1=0.03x+2(0≤x≤2000).
设L2的解析式为y2=k2x+20,
由图像得26=500k2+20,解得k2=0.012.
∴y2=0.012x+20(0≤x≤2000).
(2)当y1=y2时,两种灯的费用相等,
∴0.03x+2=0.012x+20,解得x=1000.
∴当照明时间为1000h时,两种灯的费用相等.
(3)最省钱的用灯方法:
节能灯使用2000h,白炽灯使用500h.
提示:本题的第(2)题,只要求出L1与L2交点的横坐标即可.第(1)题中,求出L1与L2的解析式,一定不能忽略自变量x的取值范围,这为第(3)题的分析、设计方案作了铺垫.在第(3)题中,当x>1000h时,L2在L1的下方,即采用节能灯省钱,因x最多为2000h,故求以下的500h应采用白炽灯.
2.解析:对于两个一次函数y1=k1x+b1,y2=k2x+b2而言:
(1)当k1≠k2时,两直线相交.
(2)当k1=k2,且b1≠b2时,两直线平行.
(3)当k1=k2,且b1=b2时,两直线重合.
故对两直线a1x+b1y=c1与a2x+b2y=c2来说:
(1)当 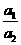 ≠
≠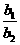 时,两直线相交,即方程组
时,两直线相交,即方程组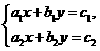 有唯一解.
有唯一解.
(2)当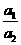 =
=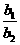 ≠
≠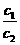 时,方程组
时,方程组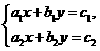 无解,两直线平行.
无解,两直线平行.
(3)当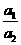 =
=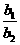 =
=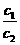 时,方程组
时,方程组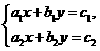 有无数多个解,两直线重合.
有无数多个解,两直线重合.
提示:方程组的解就是两个一次函数的交点坐标,当两直线只有一个公共点时,方程组有唯一解;当两直线平行(无公共点)时,方程组无解;当两直线有无数个公共点时,方程组有无数多个解.
1.(1)设L的关系式为y=kx+b,把(2,3),(-1,-3)分别代入,
得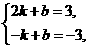 解得
解得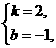
∴L1的解析式为y=2x-1.
当x=-2时,y=-4-1=5,即a=-5.
(2)设L2的关系式为y=kx,把(2,-5)代入得-5=2k,k=-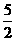 ,
,
∴L1的关系式为y=-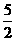 x.
x.
 ∴(-2,a)是方程组
∴(-2,a)是方程组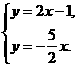 的解.
的解.
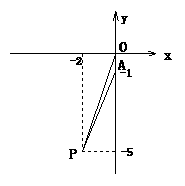
(3)如答图,把x=0代入y=2x-1,得y=-1.
∴点A的坐标为A(0,-1).
又∵P(-2,-5),
∴S△APO=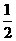 ·OA·2=
·OA·2=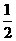 ×│-1│×2=
×│-1│×2=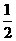 ×1×2=1.
×1×2=1.
3.解析:设L1的解析式为y=k1x+b1,
把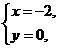
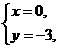 分别代入,
分别代入,
得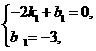 解得
解得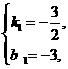
∴L1的解析式为y=-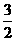 x-3.
x-3.
设L2的解析式为y=k2x+b2,把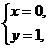
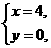 分别代入,
分别代入,
得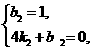 解得
解得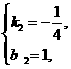
∴L的解析式为y=-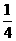 x+1.
x+1.
解方程组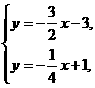 得
得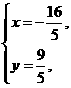
∴L1与L2的交点坐标为(-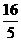 ,
,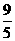 )。
)。
探究应用拓展性训练答案:
2.解析:(1)图像如答图所示.
(2)y=x+2与y=x-3的图像平行.
(3)y=x+2即x-y=-2,y=x-3即x-y=3.
∵直线y=x+2与y=x-3无交点,
∴方程组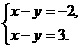 无解.
无解.
提示:当两直线平行时无交点,即由两个函数解析式组成的二元一次方程组无解.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com