
题目列表(包括答案和解析)
28.已知:如图,△ABC,∠C=900,AC=4,BC=3,AB=5。PQ∥AB,点P在AC上(与点A、C不重合),点Q在BC上。
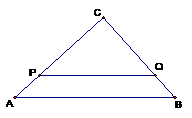 试问:在AB上是否存在点M,使得PQM为等腰直角三角形?若不存在,请简要说明理由;若存在,请求出PQ的长。
试问:在AB上是否存在点M,使得PQM为等腰直角三角形?若不存在,请简要说明理由;若存在,请求出PQ的长。

阜宁县明达中学命题人:王林 初二数学
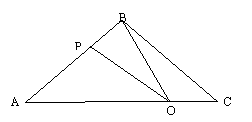
27.如图,已知,在△ABC中,BA=BC=20㎝,AC=30㎝,点P从A点出发,沿AB以4㎝/s的速度向点B运动;同时点Q从C点出发,沿CA以3㎝/s的速度向A点运动,设运动时间为x,
(1)当x为何值时,PQ∥BC;
(2)当S△BCQ∶S△ABC=1∶3时,求S△BPQ∶S△ABC的值;
(3)△APQ能否与△CQB相似,若能,求出AP的长,若不能,请说明理由.
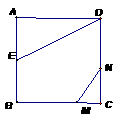
26.如图正方形ABCD的边长为2,AE=EB,线段MN的两端点分别在CB、CD上滑动,且MN=1,当CM为何值时△AED与以M、N、C为顶点的三角形相似?
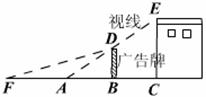
25.如图所示,在房子外的屋檐E处安有一台监视器,房子前有一面落地的广告牌,那么监视器的盲区在△ABD。已知房子上的监视器高3m,广告牌高为1.5m,广告牌距离房子5m,则盲区的长度为多少?
24.如图,⊿ABC是等边三角形,点D,E分别在BC,AC上,且BD=CE,AD与BE相交于点F.
(1)试说明⊿ABD≌⊿BCE.
(2)⊿AEF与⊿ABE相似吗?说说你的理由.
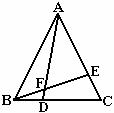 (3)BD2=AD·DF吗?请说明理由.
(3)BD2=AD·DF吗?请说明理由.
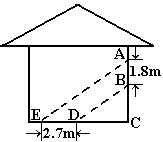
23.中午旅游团将在这里休息,阳光通过窗口照射到室内,在地面上留下2.7m宽的亮区(如图所示),已知亮区到窗口下的墙脚距离EC=8.7m,窗口高AB=1.8m,求窗口底边离地面的高BC.
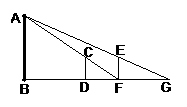
22.如图,AB(底部B不能直接到达)是途中的一个景点,小明想测出塔的高度,于是,小明在点D处测得自己的影长DF=3m,沿BD方向到达点F处再测得自己的影长FG=4m.如果小明的身高为1.6m,求路灯杆AB的高度.
21.这是一条有古老传说的河。运用三角形相似的知识,请你设计一个方案测量一条河流的宽度AB(画出示意图,并简要说明理由).
20.如图,∠ACB=∠ADC=90°,BC=a,AC=b,AB=c,要使⊿ABC∽⊿CAD,只要CD等于( )
A.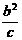 B.
B.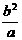 C.
C.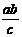 D.
D.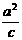
19.在△ABC与△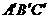 中,有下列条件:①
中,有下列条件:①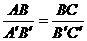 ;⑵
;⑵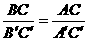 ③∠A=∠
③∠A=∠ ;④∠C=∠
;④∠C=∠ 。如果从中任取两个条件组成一组,那么能判断△ABC∽△
。如果从中任取两个条件组成一组,那么能判断△ABC∽△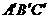 的共有( )组。
的共有( )组。
A、1 B、2 C、3 D、4
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com