
题目列表(包括答案和解析)
1.x·x3= .
30、为了美化校园环境,争创绿色学校,某区教育局委托园林公司对A,B两校进行校园绿化,已知A校有如图(1)的阴影部分空地需铺设草坪,B校有如图(2)的阴影部分空地需铺设草坪,在甲、乙两地分别有同种草皮3500米2和2500米2出售,且售价一样,若园林公司向甲、乙两地购买草皮,其路程和运费单价表如下:
路程、运费单价表
|
|
A校 |
B校 |
||
|
路程(千米) |
运费单价(元) |
路程(千米) |
运费单价(元) |
|
|
甲地 |
20 |
0.15 |
10 |
0.15 |
|
乙地 |
15 |
0.20 |
20 |
0.20 |
(注:运费单价表示每平方米草皮运送1千米所需的人民币)
求:(1) 分别求出图1、图2的阴影部分面积;
(2) 若园林公司将甲地3500m2的草皮全部运往A校,请你求出园林公司运送草皮去A、B两校的总运费;
 (3) 请你给出一种运送方案,使得园林公司支付出送草皮的总运费不超过15000元。
第30题图
(3) 请你给出一种运送方案,使得园林公司支付出送草皮的总运费不超过15000元。
第30题图
例7(2002陕西)如图1,在长为a 的正方形中挖掉一个边长为b的小正方形(a>b)把余下的部分剪拼成一个矩形(如图2),通过计算两个图形(阴影部分)的面积,验证了一个等式,则这个等式是( D )
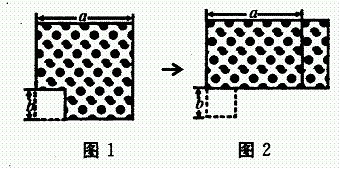
A.a2-b2=(a十b)(a-b)
B.(a+b)2=a2+2ab 十b2
C.(a-b)2=a2-2ab+b2
D.(a十2b)(a-b)==a2+ab -2b2
分析:图1表示的是a2-b2,图2表示的是(a十b)(a-b),两者面积相等,所以a2-b2=(a十b)(a-b).
故选A.
例8(2002年山东省济南市中考题)请你观察图3,依据图形面积间的关系,不需要添加辅助线,便可得到一个你非常熟悉的公式,这个公式是_____________.
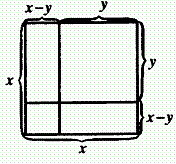
图3
分析:图中所表示的整个正方形的面积是x2,两个小正方形的面积分别是y2与(x-y)2,利用这些数据关系,结合图形便可以写出以下公式:
x2-2xy+y2 = (x-y)2,或者x2-y2 = (x+y)(x-y).
当然,在没有限定的情况下,也能写成乘法公式.
根据几何图形的特征,研究其中蕴含的数学公式,是“数形结合思想”的具体体现.
例9(2003山西)有若干张如图4所示的正方形和长方形卡片,
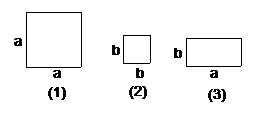
图4
表中所列四种方案能拼成边长为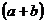 的正方形的是( )
的正方形的是( )
    卡片
卡片数量(张) 方案 |
(1) |
(2) |
(3) |
|
A |
1 |
1 |
2 |
|
B |
1 |
1 |
1 |
|
C |
1 |
2 |
1 |
|
D |
2 |
1 |
1 |
分析:此题的本意就是判断哪些卡片的面积之和是(a+b)2.
因为a2+2ab+b2=(a+b)2,对照图4所示的正方形和长方形卡片,可知三种卡片的面积分别为a2、b2和ab,它们分别需要1张、1张、2张. 由此可选出正确答案为A.
例10(2003山西太原)如图5是用四张全等的矩形纸片拼成的图形,请利用图中空白部分的面积的不同表示方法写出一个关于a、b的恒等式
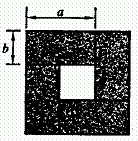
图5
分析:外框围成的大正方形面积为(a+b)2,4个矩形的面积之和为4ab,中间的空白部分的面积为(a-b)2.于是,可以列出等式(a+b)2-4ab = (a-b)2.
对于它的正确性,可以用因式分解的方法证明:
(a+b)2-4ab =a2+2ab+b2-4ab = a2-2ab+b2 = (a-b)2.
29、在通常的日历牌上,可以看到一些数所满足的规律,表1是2005年6月份的日历牌。
|
|
星期日 |
星期一 |
星期二 |
星期三 |
星期四 |
星期五 |
星期六 |
|
|
|
|
1 |
2 |
3 |
4 |
|
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
12 |
13 |
14 |
15 |
16 |
17 |
18 |
|
19 |
20 |
21 |
22 |
23 |
24 |
25 |
|
26 |
27 |
28 |
29 |
30 |
|
|
(1) 在表1中,我们选择用如表2那样2×2的长方形框任意圈出2×2个数,将它们交叉相乘,再相减,如:2×8-1×9=7,14×20-13×21=7,24×18-17×25=7,你发现了什么?再选择几个试试,看看是否都是这样,想一想,能否用整式的运算加以说明。
(2) 如果选择用如表3那样3×3的长方形方框任意圈出3×3个数,将长方形方框四解位置上的4个数交叉相,再相减,你发现了什么?请说明理由。
例5(2003福建南平)请写出一个三项式,使它能先提公因式,在运用公式来分解.
你编写的三项式是_______________,分解因式的结果是________________.
分析:利用整式乘法与因式分解的互逆关系,可以先利用乘法公式中的完全平方公式,写出一个等式,在它的两边都乘一个因式,比如
2m(m+n)2 = 2m(m2+2mn+n2)=2m3+2m2n+2mn2,
3a(2x-5y)2=3a[(2x)2-2×2x×5y+(5y)2]=3a(4x2-20xy+25y2)=12ax2-60axy+75ay2,等等.
于是编写的三项式可以是2m3+2m2n+2mn2,分解因式的结果是2m(m+n)2;
或者编写的三项式可以是12ax2-60axy+75ay2,分解因式的结果是3a(2x-5y)2,等等.
例6(2003四川)多项式9x2 + 1加上一个单项式后,使它能成为一个整式的完全平方,那么加上的单项式可以是_________________________(填上一个你认为正确的即可).
分析:根据完全平方公式a2±2ab+b2= (a±b)2的特点,若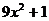 表示了a2+b2的话,则有a=3x,b=1,所以,缺少的一项为±2ab=±2(3x)·1=±6x,此时,9x2 + 1±6x=(3x±1)2;如果认为9x2 + 1表示了2ab+b2的话,则有a=4.5x2,b=1,所以,缺少的一项为a2=(4.5x)2= 20.25x4,此时,20.25x4+9x2 + 1=(4.5x2+1)2.
表示了a2+b2的话,则有a=3x,b=1,所以,缺少的一项为±2ab=±2(3x)·1=±6x,此时,9x2 + 1±6x=(3x±1)2;如果认为9x2 + 1表示了2ab+b2的话,则有a=4.5x2,b=1,所以,缺少的一项为a2=(4.5x)2= 20.25x4,此时,20.25x4+9x2 + 1=(4.5x2+1)2.
从另外一个角度考虑,“一个整式的完全平方”中所指的“整式”既可以是上面所提到的多项式,也可以是单项式. 注意到9x2=(3x)2,1=12,所以,保留二项式9x2 + 1中的任何一项,都是“一个整式的完全平方”,故所加单项式还可以是-1或者 - 9x2,此时有9x2 + 1-1=9x2=(3x)2,或者9x2 + 1-9x2=12.
综上分析,可知所加上的单项式可以是±6x、20.25x4、-1或者 - 9x2.
为了解决这个问题,我们考察个位上的数字是5的自然数的平方,任意一个个位数为5的自然数可写成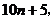 即求
即求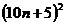 的值(n为正整数),你分析n=1、n=2,…这些简单情况,从中探索其规律,并归纳、猜想出结论(在下面的空格内填上你探索的结果)。
的值(n为正整数),你分析n=1、n=2,…这些简单情况,从中探索其规律,并归纳、猜想出结论(在下面的空格内填上你探索的结果)。
(1)通过计算,探索规律
152=225 可写成10×1×(1+1)+25
252=625 可写成10×2×(2+1)+25
352=1225 可写成10×3×(3+1)+25
452=2025 可写成10×4×(4+1)+25
…
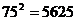 可写成
。
可写成
。
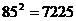 可写成
。
可写成
。
(2)从第(1)题的结果归纳、猜想得: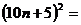 。
。
(3)根据上面的归纳、猜想,请算出: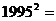 。
。
例3(2002福建福州)观察下列各式:l2+1=1×2,22+2=2×3,32+3=3×4,……
请你将猜想到的规律用自然数n(n≥1)表示出来 .
分析:根据题意,不难猜想到规律:n2+n=n(n+1).
这个结论就是用提公因式法把n2+n进行了因式分解.
例4(2003青海)请先观察下列算式,再填空:
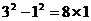 ,
,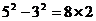 .
(1)
.
(1)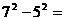 8×
;
(2)
8×
;
(2)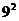 -( )
-( )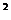 =8×4;
(3)( )
=8×4;
(3)( )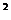 -9
-9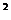 =8×5;
(4)
=8×5;
(4)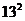 -( )
-( )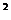 =8× ;……
通过观察归纳,写出反映这种规律的一般结论:
.
=8× ;……
通过观察归纳,写出反映这种规律的一般结论:
.
分析:类比各式,可以发现:
(1)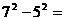 8× 3 ;
(2)
8× 3 ;
(2)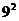 -( 7)
-( 7)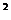 =8×4;
(3)( 11 )
=8×4;
(3)( 11 )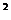 -9
-9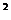 =8×5;
(4)
=8×5;
(4)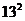 -( 11 )
-( 11 )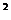 =8× 7 ;……
通过观察归纳,得到这种规律的一般结论是两个连续奇数的平方差能被8整除(或说是8的倍数).
=8× 7 ;……
通过观察归纳,得到这种规律的一般结论是两个连续奇数的平方差能被8整除(或说是8的倍数).
如果我们分别用2n+1和2n-1表示两个相邻的奇数,则利用平方差公式,有
(2n+1)2 – (2n-1)2 = [(2n+1)+(2n-1)] [(2n+1)-(2n-1)] = 4n×2 = 8n.
例1(2004山西)已知x+y=1,那么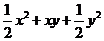 的值为_______.
的值为_______.
分析:通过已知条件,不能分别求出x、y的值,所以要考虑把所求式进行变形,构造出x+y的整体形式. 在此过程中我们要用完全平方公式对因式分解中的.
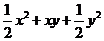 =
=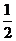 (x2+2xy+y2)=
(x2+2xy+y2)=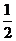 (x+y)2 =
(x+y)2 = 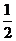
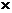 12 =
12 = 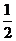
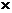 1 =
1 = 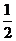 .
.
在此过程中,我们先提取公因式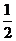 ,再用完全平方公式对原式进行因式分解,产生x+y的整体形式,最后将x+y=1代入求出最终结果.
,再用完全平方公式对原式进行因式分解,产生x+y的整体形式,最后将x+y=1代入求出最终结果.
例2(2004广西桂林)计算: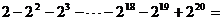 ___________.
___________.
分析:为了便于观察,我们将原式“倒过来”,即
原式 = 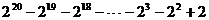
= 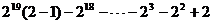
= 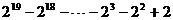
= 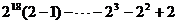
= 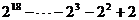
= ……
= 22 + 2 = 4+2 = 6.
此题的解题过程中,巧妙地用到了提公因式法进行分解因式,使结构特点明朗化,规律凸现出来. 此题解法很多,比如,我们还可以采用整体思想,把原式看作一个整体,利用方程与提公因式法分解因式相结合的方法解答此题.
设M = 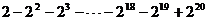 ,则-M =
,则-M = 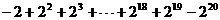
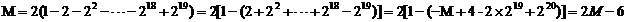
即
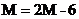 .
.
解得
M = 6.
3、通过乘法公式:(a + b)(a - b)=a2 - b2,(a±b)2= a2±2ab + b2的逆向变形,进一步发展观察、归纳、类比、概括等能力,发展有条理思考及语言表达能力.
在中考中,除了考查对一个整式进行分解因式等常规题型外,因式分解作为一种重要的解题方法和工具,经常出现于各种题型中,以下几种就值得引起注意.
2、了解因式分解的意义,会用提公因式法、平方差公式和完全平方公式(直接用公式不超过两次)进行因式分解(指数是正整数).
1、经历探索分解因式方法的过程,体会数学知识之间的整体(整式乘法与因式分解)联系.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com