2. 两边和它们的夹角对应相等的两个三角形全等(可以简写成“边角边”或“SAS”).

1. 三边对应相等的两个三角形全等(可以简写成“边边边”或“SSS”).

全等形：能够完全重合的图形叫做全等形.

全等三角形：能够完全重合的两个三角形叫做全等三角形.

对应顶点、对应边、对应角：把两个全等的三角形重合到一起.重合的顶点叫做对应顶点；重合的边叫做对应边；重合的角叫做对应角.

23、某公司在甲、乙两座仓库分别有农用车12辆和6辆，现需要调往A县10辆，调往B县8辆．已知从甲仓库调运一辆农用车到A县和B县的运费分别为40元和80元；从乙仓库调运一辆农用车到A县和B县的运费分别为30元和50元．

(1)设从乙仓库调往A县农用车x辆，求总运费y关于x的函数关系式；

(2)若要让总运费不超过900元，问共有几种调运方案；

(3)求出总运费最低的调运方案，最低运费是多少？

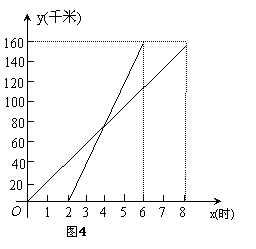
22、如图4表示一艘轮船与一艘快艇沿相同路线从甲港到乙港行驶过程中路程随时间变化的图象(分别是正比例函数图象和一次函数图象).根据图象解答下列问题：

(1) 快艇出发多长时间赶上轮船？

(2)轮船和快艇在途中(不包括起点和终点)行驶的速度分别是多少？

(3)请求出表示轮船行驶过程的函数解析式(不需写出自变量取值范围)；

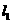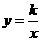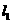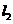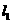21、用表示反比例函数在第一象限内的图象，已知图象过点A(2，1)，图象与关于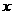轴对称，试求图象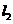的函数解析式(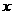>0)

20、利用一次函数的图象，求方程组的解

19、一次函数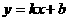的图象经过点(0，-3)、(2，-1).

(1)求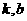的值；

(2)若直线经过点A(-2,a)，求a的值．

18、已知点P(x₁，y₁)和点Q(x₂，y₂)在函数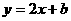的图象上，若x₁>x_2，

比较大小y₁　　　　 y_2。(填“>”、“=”、“<” )．

17、已知一次函数的图象经过点P(2，－3)，写出一个符合条件的一次函数的解析式　　　　　　　　　　　　　　　 　．