1.计算：＝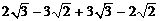　　　

4.3二次根式的加、减法

知识网络：

二次根式加减运算法则：①将二次根式化成最简二次根式；

②将被开方数相同的二次根式进行合并.

基础训练

3．为美化校园，学校准备在一块圆形空地上建花坛，现征集设计方案，要求设计的图案由圆、三角形、矩形组成(三种几何图案的个数不限)，并且使整个圆形场地成轴对称图形，请你画出你的设计方案．

　　 答案：略。毛

2．已知a⊥b，a、b相交于点O，点P为a、b外一点．

求作：点P关于a、b的对称点M、N，并证明OM=ON(不许用全等)．

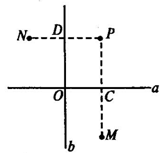
　　 作法：(1)过点P作PC⊥a，并延长PC到M，使CM=PC．

　　 (2)过点P作PD⊥b，并延长PD到N，使得DN=PD．

　　 则点M、N就是点P关于a、b的对称点．

　　 证明：∵点P与点M关于直线a对称，

　　 ∴直线a是线段PM的中垂线．

　　 ∴OP=OM．

　　 同理可证：OP=ON．

　　 ∴OM=ON．

1．已知△ABC，过点A作直线L．

求作：△A′B′C′使它与△ABC关于L对称．

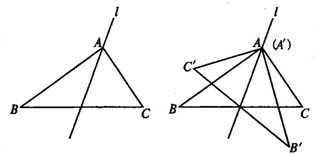
　　 作法：(1)作点C关于直线L的对称点C′；

　　 (2)作点B关于直线L的对称点B′；

　　 (3)点A在L上，故点A的对称点A′与A重合；

　　 (4)连结A′B′、B′C′、C′A′．

　　 则△A′B′C′就是所求作的三角形．

12.2作轴对称图形

3．已知A，B两点是平面直角坐标系内不同的两点，A(x，3)，B(4，y)，如果AB∥x轴，求x，y的值.

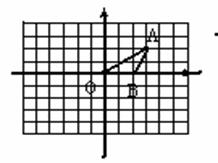　 4.如图，作△ABC关于x轴对称的像，然后向下平移3个单位，求此时三角形各顶点的坐标.

拓展思考:

我们知道点P(x,y)关于X轴的对称点坐标是(x,-y),点P(x,y)关于Y 轴的对称点坐标是(-x,y),类似地可以得到点P(x,y)关于原点的对称点的坐标是(-x,-y),你能说明这条规律吗?并求出点(m,n)分别关于X轴、Y轴、原点的对称点的坐标.

火眼金睛:

已知点P的坐标是(-4 ，3),先将点P作X轴的轴对称变换得点P₁，再将P₁作平移变换,向右平移8个单位得P₂,则PP₂的距离是10.你认为对吗?说明你的理由.

2.选择题:

(1) 点A(3，-4)向左平移3个单位的象的坐标是(　　 )

　　 (A)(6，-4)　　 (B)(0，-4)　　　 (C)(3，-1)　　　 (D)(3，-7)

(2)点M(-5，y)向下平移5个单位的象关于x轴对称，则y的值是(　　 )

　　 (A)-5　　　　　 (B)5　　　　　　　 (C)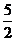　　　　　　　 (D)-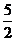

(3)把点P(-x，y)变为Q(x，y)，只需(　　 )

　　　 (A) 向左平移2x个单位　　　　　　 (B) 向右平移2x个单位　　　　　　

　(C) 作关于x轴对称　　　　　　　 (D) 作关于y轴对称

1.填空题:

(1)点A(-2，4)向左平移3个单位的象的坐标是　　　　 .

(2)点A(2，1)向右平移5个单位，再向下平移3个单位的象的坐标是　　　　 .

(3)点P(-2，0)向　　 平移　　 个单位，则向　　 平移　　 个单位的象的坐标是(3，-1)

4.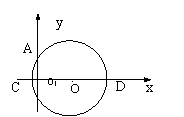如图，圆O₁的圆心在x轴上，半径是5，OO₁=3，写出圆与各坐标轴交点的坐标，点A与点B的坐标有什么关系？

基础训练: