3.如下左图，在菱形ABCD中，AE⊥BC于点E，AF⊥CD于点F，且E、F分别为BC、CD的中点，(如图1)则∠EAF等于(　　 )

A.75°　 B.60°　 C.45°　 D.30°

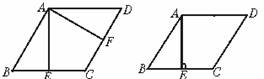
2.菱形的周长为12 cm，相邻两角之比为5∶1,那么菱形对边间的距离是(　　 )

A.6 cm　 B.1.5 cm　　 C.3 cm D.0.75 cm

1.下列命题中，真命题是(　　 )

A.对角线互相垂直且相等的四边形是菱形

B.对角线互相垂直的平行四边形是菱形

C.对角线互相平分且相等的四边形是菱形

D.对角线相等的四边形是菱形

24.8 角平分线的性质及其逆定理

第1题. 如图，△ABC中，AD为∠BAC的平分线，DE⊥AB，DF⊥AC，E、F为垂足，在以下结论中：①△ADE≌△ADF；②△BDE≌△CDF；③△ABD≌△ACD；④AE=AF；⑤BE=CF；⑥BD=CD．其中正确结论的个数是(　)

A．1　　 B．2　　 C．3　　 D．4

答案：B．

第2题. 如图，Rt△ABC中，∠C=90º，BD是角平分线，DE⊥AB，垂足为E，BC=6，CD=3，AE=4，则DE=_______，AD=_______，△ABC的周长是_______．

答案：3，5，24

第3题. 用三角尺画角平分线：如图，∠AOB是一个任意角，在边OA，OB上分别取OM=ON，再分别过M、N作OA，OB的垂线，交点为P，画射线OP，则这条射线即为角平分线．请解释这种做法的道理．你还能举出哪些作角平分线的方法，并说明这种做法的道理．

答案：提示：OM=ON，OP=OP，∴Rt△OMP≌Rt△ONP(HL)，∴∠MOP=∠NOP，∴射线OP是∠AOB的平分线．

第4题. 求证：三角形的三条角平分线相交于一点．

答案：提示：画出图形，写出已知、求证，证明两条角平分线的交点到第三个角的两边的距离相等．

第5题. 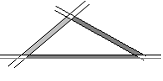如图，三条公路围成的一个三角形区域，要在这个区域中建一个加油站，使它到三条公路的距离都相等，加油站应建在什么位置？请用尺规作图，找出建造加油站的位置．

答案：提示：作两个角的平分线，交点即为建加油站的位置．

第6题. 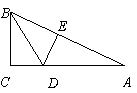如图，△ABC中，∠C=90º，BD平分∠ABC交AC于D，DE是AB的垂直平分线，DE=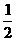BD，且DE=1.5cm，则AC等于(　)

A．3cm　 B．7.5cm　　 C．6cm　 D．4.5cm

答案：D．

第7题. 如图，△ABC中，P是角平分线AD，BE的交点．

求证：点P在∠C的平分线上．

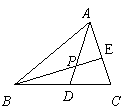
答案：如图，过点P作PM⊥AB，PN⊥BC，PQ⊥AC，垂足分别为M、N、Q．∵P在∠BAC的平分线AD上，∴PM=PQ．P在∠ABC的平分线BE上，∴PM=PN。∴PQ=PN，∴点P在∠C的平分线．

第8题. 如图，已知点D是∠ABC的平分线上一点，点P在BD上，PA⊥AB，PC⊥BC，垂足分别为A，C．

求证：(1)AD=CD；(2)∠ADB=∠CDB．

答案：△ABP≌△CBP，∴AB=CB，又∠ABP=∠CBP，BD=BD，∴△ABD≌△CBD，∴AD=CD，∠ADB=∠CDB．

第9题. 如图，在∠AOB的两边OA，OB上分别取OM=ON，OD=OE，DN和EM相交于点C．

求证：点C在∠AOB的平分线上．

答案：提示：作CE⊥OA于E，CF⊥OB于F，OM=ON，OE=OD，∠MOE=∠NOD，∴△MOE≌△NOD(SAS)，∴S_{△M O E} =S_{△N O D}，同时去掉S_{四边形ODCE}，得S_{△M D C}=S_{△N E C}，易证，MD=NE，∴CE=CF，∴点C在∠AOB的平分线上．

第10题. 已知：如图，AD是△ABC的角平分线，DE⊥AB，DF⊥AC，E、F分别为垂足．

求证：AD垂直平分EF．

答案：提示：由角平分线的性质定理，可得DE=DF，进而求得∠DEF=∠DFE，∠AEF=∠AFE，所以AE=AF，所以AD垂直平分EF．

第11题. 如图，已知△ABC中，∠C=90º，∠BAC=2∠B，D是BC上一点，DE⊥AB于E，DE=DC．

求证：AD=BD．

答案：提示：DE=DC，AD=AD，∴Rt△ADE≌Rt△ADC，∴∠EAD=∠DAC=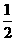∠BAC，又∠B=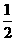∠BAC，∴∠EAD=∠B，∴AD=BD．

如图2，小明，小华用四张扑克牌玩游戏，他俩将扑克牌洗均匀后，背面朝上放置在桌面上，小明先抽，小华后抽，抽出的牌不放回．

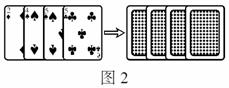
(1)若小明恰好抽到的是黑桃4．

①请绘制这种情况的树状图；

②求小华抽出的牌的牌面数字比4大的概率．

(2)小明、小华约定：若小明抽到的牌的牌面数字比小华的大，则小明胜；反之，则小明负，你认为这个游戏是否公平？说明你的理由．

5．(本题14分)这是一个抛掷三个筹码的游戏．准备三个筹码，第一个一面画上×，另一面画上d；第二个一面画上d，另一面画上#；第三个一面画上#，另一面画上×．甲、乙两人中一人抛掷三个筹码，另一人记录每次游戏谁赢．

游戏规则：掷出的三个筹码中有一对的(××或dd或##)，甲方赢；否则，乙方赢．你认为这个游戏公平吗？若不公平，谁赢的机会大？试通过计算来说明．

4．(本题12分)某校八年级将举行班级乒乓球对抗赛，每个班必须选派出一对男女混合双打选手参赛．八年级一班准备在小娟、小敏、小华三名女选手和小明、小强两名男选手中，选男、女选手各一名组成一对选手参赛，一共能够组成哪几对？如果小敏和小强的组合是最强组合，那么采用随机抽签的办法，恰好选出小敏和小强参赛的概率是多少？

3．(本题10分)如图1是从一副扑克牌中取出的两组牌，分别是黑桃1，2，3，4和方块1，2，3，4，将它们背面朝上分别重新洗牌后，从两组牌中各摸出一张，那么摸出的两张牌的牌面数字之和等于5的概率是多少？请你用列举法(列表或画树状图)加以分析说明．

2．(本题10分)某个地区几年内的新生婴儿数及其中男婴数统计如下表：

时间范围	1年内	2年内	3年内	4年内
新生婴儿数(n)	5545	9607	13520	17190
男婴数(m)	2825	4900	6925	8767
男婴出生频率()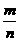

请回答下列问题：

(1)填写上表各年的男婴出生频率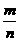．(结果都保留三个有效数字)

(2)在大量重复进行同一试验时，事件A发生的频率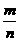总是接近于某个常数并在它的附近摆动，我们把这个常数叫做事件A的概率，记作PA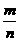．= ．根据(1)填写的结果及以上说明，这一地区男婴出生的概率P(A)=　　．

1．(本题10分)某射击运动员在同一条件下进行练习，结果如下表所示：

射击次数n	10	20	50	100	200	500	1 000	2 000
击中10环次数m	8	19	44	93	178	453	899	1 802
击中10环频率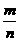

(1)计算表中击中10环的各个频率；

(2)这名运动员射击一次，击中10环的概率约为多少？