
题目列表(包括答案和解析)
6.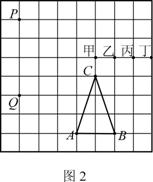 如图2,若A、B、C、P、Q、甲、乙、丙、丁都是方格纸中的格点,为使△ABC∽△PQR,则点R应是甲、乙、丙、丁四点中的
如图2,若A、B、C、P、Q、甲、乙、丙、丁都是方格纸中的格点,为使△ABC∽△PQR,则点R应是甲、乙、丙、丁四点中的
A. 甲 B. 乙
C. 丙 D. 丁
5. 若“!”是一种数学运算符号,并且1!=1,2!=2×1=2,3!=3×2×1=6,4!=4×3×2×1,…,则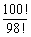 的值为
的值为
A. 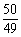 B.
99! C.
9900 D. 2!
B.
99! C.
9900 D. 2!
4. 下列命题中,正确的是
A. 同位角相等 B. 平行四边形的对角线互相垂直平分
C. 等腰梯形的对角线互相垂直 D. 矩形的对角线互相平分且相等
3. 某服装销售商在进行市场占有率的调查时,他最应该关注的是
A. 服装型号的平均数 B. 服装型号的众数
C. 服装型号的中位数 D. 最小的服装型号
2. 图1所示的几何体的右视图是

1.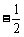 的绝对值是
的绝对值是
A. -2 B.
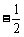 C.
2 D.
C.
2 D. 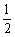
27. (本小题14分)如图,在平面直角坐标系内,⊙C与y轴相切于D
(本小题14分)如图,在平面直角坐标系内,⊙C与y轴相切于D
点,与x轴相交于A(2,0)、B(8,0)两点,圆心C在第四象限.
⑴ 求点C的坐标;
⑵ 连结BC并延长交⊙C于另一点E,若线段BE上有一点P,使得
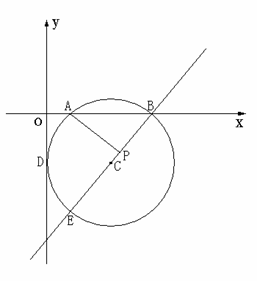 AB2=BP·BE,能否推出AP⊥BE?请给出你的结论,并说明理由;
AB2=BP·BE,能否推出AP⊥BE?请给出你的结论,并说明理由;
⑶ 在直线BE上是否存在点Q,使得AQ2=BQ·EQ?若存
在,求出点Q的坐标;若不存在,也请说明理由.
|
2005年浙江省台州市初中毕业、升学考试
26. (本小题12分)
(本小题12分)
我国古代数学家秦九韶在《数书九章》中记述了“三斜求积术”,
即已知三角形的三边长,求它的面积.用现代式子表示即为:
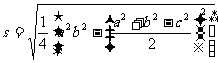 ……①(其中
……①(其中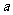 、
、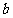 、
、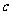 为三角形的三边长,
为三角形的三边长,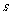 为面积).
为面积).
而另一个文明古国古希腊也有求三角形面积的海伦公式:
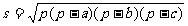 ……②(其中
……②(其中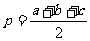 ).
).
⑴ 若已知三角形的三边长分别为5、7、8,试分别运用公式①和公式②,计算该三角形的
面积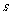 ;
;
⑵ 你能否由公式①推导出公式②?请试试.
25. (本小题12分)
(本小题12分)
如图,用长为18 m的篱笆(虚线部分),两面靠墙围成矩形的苗圃.
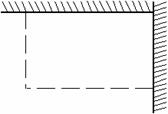 (1)设矩形的一边为
(1)设矩形的一边为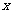 (m),面积为
(m),面积为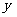 (m2),求
(m2),求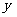 关
关
于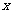 的函数关系式,并写出自变量
的函数关系式,并写出自变量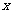 的取值范围;
的取值范围;
(2)当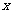 为何值时,所围苗圃的面积最大,最大面积是多少?
为何值时,所围苗圃的面积最大,最大面积是多少?
|
24. (本小题10分)
(本小题10分)
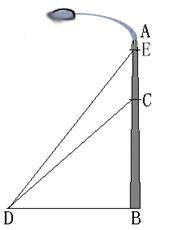
如图,我市某广场一灯柱AB被一钢缆CD固定,CD与地面成40°
夹角,且DB=5m,则 BC的长度是多少?现再在C点上方2m处
加固另一条钢缆ED,那么钢缆ED的长度为多少?(结果保留三个有效数字)
[参考数据: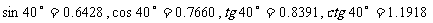 ]
]
 |
|||
|
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com