25、已知二次函数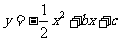的图象经过点A(－3，－6)，并与x轴交于点B(－1，0)和点C，顶点为P。

(1)　　　 求二次函数的解析式；

(2)　　　 设点D为线段OC上一点，且∠DPC=∠BAC，求点D的坐标；

说明：若(2)你经历反复探索没有获得解题思路，请你在不改变点D的位置的情况下添加一个条件解答此题，此时(2)最高得分为3分。

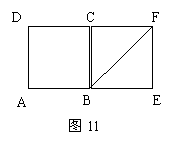
24、如图11，正方形ABCD和正方形BEFC。

操作：M是线段AB上一动点，从A点至B点移动，DM⊥MN，交对角线BF于点N。

探究：线段DM和MN之间的关系，并加以证明。

说明：如果你经历反复探索，没有找到解决问题的方法，请你把探索过程中的某种思路过程写出来(要求至少写3步)；(2)在你经历说明(1)的过程之后，可以从下列①、②中选取一个补充或更换已知条件，完成你的证明。注意：选取①完成证明得9分；选取②完成证明得6分。①M是线段AB的中点；②M、N分别是线段AB、BF的中点。

附加题

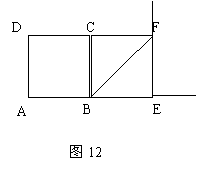
如图12，当M是线段AE延长线上一动点，DM⊥MN，交对角线BF延长线于点N，探究线段DM和MN之间的关系，并加以证明。

	A

23、如图10，把矩形OABC放置在直角坐标系中，OA＝6，OC＝8，若将矩形折叠，使点B与O重合，得到折痕EF。

(1)　　　 可以通过________办法，使四边形AEFO变到四边形BEFC的位置(填“平移”、“旋转”或“翻转”)；

(2)　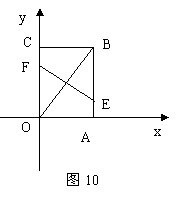　　 求点E的坐标；

(3)　　　 若直线l把矩形OABC的面积分成相等的两部分，

则直线l必经过点的坐标是______.

22、一对骰子，如果掷两骰子正面点数和为2、11、12，那么甲赢；如果两骰子正面的点数和为7，那么乙赢；如果两骰子正面的点数和为其它数，那么甲乙都不赢。继续下去，直到有一个人赢为止。

(1)　　　 你认为游戏是否公平，并解释原因；

(2)　　　 如果你认为游戏公平，那么请你设计一个不公平的游戏；如果你认为游戏不公平，那么请你设计一个公平的游戏。

21、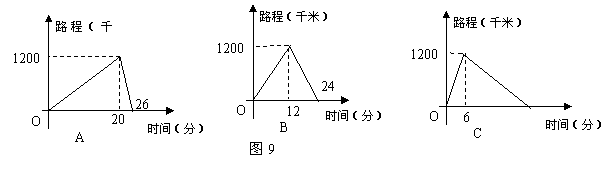小明、爸爸、爷爷同时从家里出发到达同一目的地后立即返回，小明去时骑自行车，返回时步行；爷爷去时是步行，返回时骑自行车；爸爸往返都是步行。三人步行的速度不等，小明和爷爷骑自行车的速度相等，每个人的行走路程与时间的关系如图9中的A、B、C表示，根据图象回答下列问题：

(1)　　　 三个图象中哪个对应小明、爸爸、爷爷？

(2)　　　 小明家距离目的地多远？

(3)　　　 小明与爷爷骑自行车的速度是多少？爸爸步行的速度是多少？

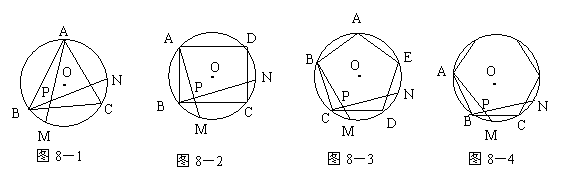
20、如图，8－1、8－2、8－3、…、8－n分别是⊙O的内接正三角形ABC，正四边形ABCD、正五边形ABCDE、…、正n边形ABCD…，点M、N分别从点B、C开始以相同的速度在⊙O上逆时针运动。

(1)　　　 求图8－1中∠APN的度数；

(2)　　　 图8－2中，∠APN的度数是_______，图8－3中∠APN的度数是________。

(3)　　　 试探索∠APN的度数与正多边形边数n的关系(直接写答案)

19、如图5，A、B两点被池塘隔开，为测量AB两点的距离，在AB外选一点C，连结AC和BC，并分别找出AC和BC的中点M、N，如果测得MN＝20m，那么AB＝2×20m＝40m。

(1)　　　 测AB距离也可由图6所示用三角形相似知识来解决，请根据题意填空：延长AC到D，使CD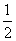＝AC，延长BC到E，使CE＝________，则由相似三角形得，AB=_______.

(2)　　　 测AB距离还可由三角形全等的知识来设计测量方案，求出AB的长，请用上面类似的方法，在图7中画出图形，并叙述你的测量方案。

18、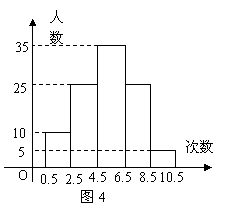为了了解某初中学生的体能情况，抽取若干名学生在单位时间内进行引体向上测试，将所得数据整理后，画出频数分布直方图(如图4)，图中从左到右依次为第1、2、3、4、5组。

(1)　　　 求抽取多少名学生参加测试？

(2)　　　 处于哪个次数段的学生数最多？(答出是第几组即可)

(3)　　　 若次数在5次(含5次)以上为达标，

求这次测试的达标率。

17、已知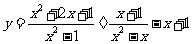。试说明不论x为何值，y的值不变。

16、如图3，已知AD∥BC，AD=CB，求证：△DAC≌△BCA.

(说明：证明过程中要求写出每步的证明依据)