4．设x₁、x₂是方程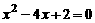的两实数根，则x₁+x₂=　　　　 ， x₁·x₂=　　　 .

3．据无锡《江南晚报》“热线话题”报道：无锡市全年的路灯照明用电约需4200万千瓦·时，这个数据用科学记数法可表示为　　　　 万千瓦·时.

2．点(1，2)关于原点的对称点的坐标为　　　　 .

1．－3的相反数是　　　 ，－3的绝对值是　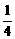　　 ，的算术平方根是　　　 .

24、(本小题满分9分)

某住宅小区，为美化环境，提高居民区生活质量，要建一个八边形居民广场(平面图如图所示)。其中，正方形MNPQ与四个相同矩形(图中阴影部分)的面积的和为800平方米。

(1)设矫形的边长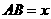(米)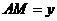，(米)，用含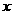的代数式表示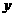为　　　　 ；

(2)现计划在正方形区域上建雕塑和花坛，平均每平方米造价为2100元；在四个相同的矩形区域上铺设花岗岩地坪，平均每平方米造价为105元；在四个三角形区域上铺设草坪，平均每平方米造价为40元；

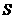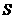①设该工程的总造价为(元)，求关于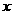的函数关系式；

②若该工程的银行贷款为235000元，问仅靠银行贷款能否完成该工程的建设任务？若能，请列出设计方案；若不能请说明理由；

③若该工程在银行贷款的基础上，又增加奖金73000元，问能否完成该工程的建设任务？若能，请列出所有可能的设计方案；若不能，请说明理由。

23、(本小题满分8分)

某学习小组在探索“各内角都相等的圆内接多边形是否为正多边形”时，进行如下：

甲同学：这种多边形不一定是正多边形，如圆内接矩形；

乙同学：我发现边数是6，它也不一定是正多边形。如图一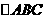，是正三角形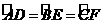，，可以证明六边形ADBECF的各角相等，但它未必是正六边形；

丙同学：我能证明，边数是5时，它是正多边形。我想，边数是7时，它可能是正多边形。

……

(1)请你说明乙同学构造的六边形各角相等；

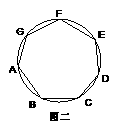
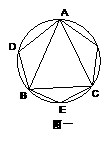(2)请你证明，各角都相等的圆内接七边形ABCDEFG(如图二)是正七边形(不必写已知、求证)；

(3)根据以上探索过程，提出你的猜想(不必证明)；

22、(本小题满分7分)

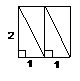如图，把边长为的正方形剪成四个全等的直角三角形。请用这四个直角三角形拼成符合下列要求的图形(全部用上，互不重叠且不留空隙)，并把你的拼法仿照图中实际大小画在方格纸内(方格为)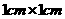

(1)不是正方形的菱形(一个)　　　 　(2)不是正方形的矩形(一个)

(3)梯形(一个)　　　 　　　　　　　(4)不是矩形和菱形的平行四边形(一个)

(5)不是梯形和平行四边形的凸四边形(一个)

21、(本小题满分7分)

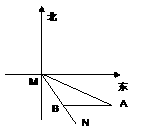如图，MN表示某引水工程的一段设计路线，从M到N的走向为南偏东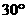，在M的南偏东方向上有一点A，以A为圆心，500米为半径的圆形区域为居民区，取MN上另一点B，测得BA的方向为南偏东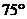，已知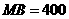米，通过计算，如果不改变方向，输水线路是否会穿过居民区？

20、(本小题满分7分)

某公司销售部有营销人员15人，销售部为了制定某种商品的月销售定额，统计了这15人某月的销售量如下：

(1)求这15位营销人员该月销售量的平均数、中位数和众数；

(2)假设销售部负责人把每位营销员的月销售额定为320件，你认为是否合理，为什么？如果不合理，请你制定一个较合理的销售定额，并说明理由；

19、(本小题满分7分)

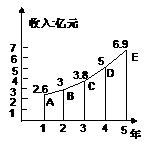
下图表示近5年来某市的财政收入情况。图中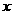轴上1，2，…，5依次表示第1年，第2年，…，第5年，即1997年，1998年，…，2001年，可以看出，图中的折线近似于抛物线的一部分。

(1)请你求出过A、C、D三点的二次函数的解析式；

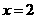(2)分别求出当和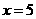时，(1)中的二次函数的函数值；并分别与B、E两点的纵坐标相比较；

(3)利用(1)中的二次函数的解析式预测今年该市的财政收入；