
题目列表(包括答案和解析)
4.现在我市人口约有4580000人,用科学记数法表示为
A.458×104 B.45.8×105 C.4.58×106 D.0.458×107
3.计算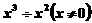 的结果为
的结果为
A.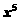 B.
B.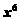 C.
C.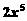 D.
D.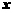
2.3的倒数为
A.-3 B.3 C.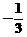 D.
D.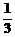
以下每小题给出的四个选项中,只有一个是符合题目要求的,请选出并把答题卡上对应题目的正确答案标号涂黑.
1.在-2,0,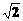 ,1,
,1,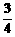 ,-0.4中,正确的个数为
,-0.4中,正确的个数为
A.2个 B.3个 C.4个 D.5个
 18.(本题满分7分)
18.(本题满分7分)
 计算:
计算: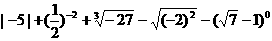
 19.(本题满分7分)先化简再求值。
19.(本题满分7分)先化简再求值。

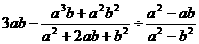
其中: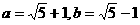
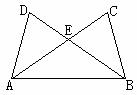
 20.(本题满分7分)已知:如图,AD=BC,∠D=∠C,AC交
BD于点E。求证:AC=BD。
20.(本题满分7分)已知:如图,AD=BC,∠D=∠C,AC交
BD于点E。求证:AC=BD。


 21.(本题满分8分)一次函数y=x+b与反比例函数
21.(本题满分8分)一次函数y=x+b与反比例函数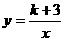 图像的交点为A(m,n),且m,n(m<n)是关于x的一元二次方程kx2+(2k-7)x+k+3的两个不相等的实数根,其中k为非负整数,m,n为常数。
图像的交点为A(m,n),且m,n(m<n)是关于x的一元二次方程kx2+(2k-7)x+k+3的两个不相等的实数根,其中k为非负整数,m,n为常数。
(1)求k的值;
(2)求A的坐标与一次函数解析式。
 22.(本题满分8分)初三(5)班综合实践小组去湖滨花园
22.(本题满分8分)初三(5)班综合实践小组去湖滨花园
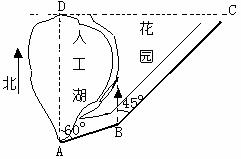
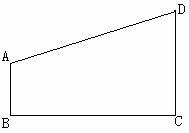
 测量人工湖的长,如图A、D是人工湖边的两座雕塑,AB、
测量人工湖的长,如图A、D是人工湖边的两座雕塑,AB、
BC是湖滨花园的小路,小东同学进行如下测量,B点在A点北偏东60o方向,C点在B点北偏东45o方向,C点在D点正东方向,且测得AB=20米,BC=40米,求AD的长。(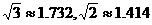 ,结果精确到0.01米)
,结果精确到0.01米)
 (本题满分10分)已知:⊙
(本题满分10分)已知:⊙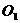 与⊙
与⊙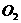 相交于A、B两点,
相交于A、B两点,
 ⊙
⊙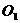 的切线AC交⊙
的切线AC交⊙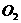 于点C。直线EF过点B交⊙
于点C。直线EF过点B交⊙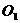 于点E,交⊙
于点E,交⊙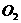 于点F。
于点F。
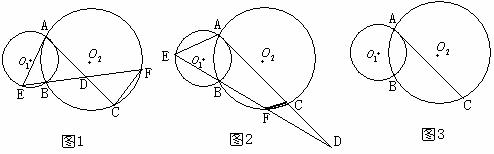
(1)若直线EF交弦AC于点K时(如图1)。求证:AE∥CF;
(2)若直线EF交弦AC的延长线于点时(如图2)。求证:DA·DF=DC·DE;
(3)若直线EF交弦AC的反向延长线于点(在图3自作),试判断(1)、(2)中的结论是否成立?并证明你的正确判断。

24.(本题满分10分)被誉为城区风景线的杭州东路跨湖段
 1857米,其各项绿化指标如表中所示,分析下表,回答下
1857米,其各项绿化指标如表中所示,分析下表,回答下
列下列问题:
|
主要树种 |
株数 |
绿化覆盖率 |
|
香樟 |
336 |
24% |
|
柳树 |
188 |
12% |
|
棕榈 |
258 |
3% |
|
桂花树 |
50 |
1% |
|
合计 |
832 |
40% |
(1)已知杭州东路全长4744米,在各树行距(两树之间的水平距离)不变的情况下,请你用统计方法估计全线栽植的香樟、棕榈各多少株(结果保留整数)?
(2)杭州东路全线绿化工程是分期完成的,每千米的绿化投资成本一定。跨湖段是首期工程,且阳光、水份、土壤皆优于其它路段,问是否可能用跨湖段的绿化覆盖率40%表示全线的绿化覆盖率?请用统计知识说明理由。
 25.(本题满分12分)如图,在直角梯形ABCD中,AB∥
25.(本题满分12分)如图,在直角梯形ABCD中,AB∥
 CD,∠ABC=90o,AB=4,BC=
CD,∠ABC=90o,AB=4,BC=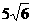 ,CD=9。
,CD=9。
(1)在BC边上找一点O,过O点作OP⊥BC交AD于P,且OP2=AB·DC。求BO的长;
(2)以BC所在直线为x轴,OP所在直线为y轴,建立平面直角坐标系,求经过A、O、D三点的抛物线的解析式,并画出引抛物线的草图;
 (3)在(2)中的抛物线上,连结AO、DO,证明:△AOD为直角三角形;过P点任作一直线与抛物线相交于A/(x1,y1),D/(x2,y2)两点,连结A/O、B/O,试问:△A/O/D/还为直角三角形吗?请说明理由。
(3)在(2)中的抛物线上,连结AO、DO,证明:△AOD为直角三角形;过P点任作一直线与抛物线相交于A/(x1,y1),D/(x2,y2)两点,连结A/O、B/O,试问:△A/O/D/还为直角三角形吗?请说明理由。
湖北省黄石市2005年初中升学统一考试
17.矩形ABCD中,AB=8,BC=15,如果分别以A、C为圆心的两圆相切,点D在⊙C内,点B在⊙C外,那么⊙A的半径r的取值范围是_____________。
16.民意商场对某种商品作调价,按原价8折出售,此时商品的利润率是10%,此商品进价为1000元,则商品的原价是_____________。
15.分解因式: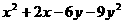 =_____________________________。
=_____________________________。
14.已知菱形的周长为40cm,两条对角线之比为3∶4,则菱形面积为_______。
13.若最简根式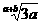 与
与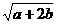 是同类二次根式,则
是同类二次根式,则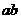 =___________。
=___________。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com