
题目列表(包括答案和解析)
1. 已知(z-x)2-4(x-y)(y-z)=0,求证:x,y,z成等差数列 (“已知”是哪一个方程的
⊿=0?)
13、27° 14、a+b 15、-1/4 16、3.7,1.85 17、32+x=2(28-x) 18、24
二、选择题(本题满分30分,每小题3分)
19、C 20、D 21、C 22、A 23、A 24、B 25、C 26、B 27、C 28、D
三、(本题满分15分,每小题5分)
29、解:去分母得 4(x-2)≥3x-5
去括号,得 4x-8≥3x-5 2分
移项,得 4x-3x≥-5+8 3分
合并同类项,得x≥3 4分
这个不等式的解集在数轴上表示如下 5分
 30、解:(1)∵x=-2时, y=-3 1分
∴-3=k/-2+1
∴k=3 3分
(2)由(1),得 y=3/(x+1)
∴当x=1/2时,y=3/(x+1)=2 5分
31、解:由中位线定理,得(2+BC)/2=5
∴BC=8 2分
∵四边形ABCD是等腰梯形
∴BE=(BC-AD)/2=(8-2)/2=3 3分
在Rt△AEB中,AB=
30、解:(1)∵x=-2时, y=-3 1分
∴-3=k/-2+1
∴k=3 3分
(2)由(1),得 y=3/(x+1)
∴当x=1/2时,y=3/(x+1)=2 5分
31、解:由中位线定理,得(2+BC)/2=5
∴BC=8 2分
∵四边形ABCD是等腰梯形
∴BE=(BC-AD)/2=(8-2)/2=3 3分
在Rt△AEB中,AB=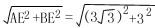 =6(cm) 5分
四、(本题满分5分)
32、解法一:设年利率是5%和4%的两种储蓄分别存了x元和y元,依题意,得
=6(cm) 5分
四、(本题满分5分)
32、解法一:设年利率是5%和4%的两种储蓄分别存了x元和y元,依题意,得
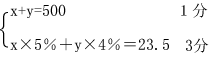 解这个方程组得
x=350,y=150 4分
答:年利率是5%和4%的两种储蓄分别存了350元和150元。 5分
解法二:设年利率是5%的储蓄存了x元,则年利率是4%的储蓄了(500-x)元
依题意,得x×5%+(500-X)×4%=23.5 3分
解这个方程,得x=350 ∴500-x=150 4分
答:年利率是5%和4%的两种储蓄分别存了350元和150元。 5分
五、(本题满分5分)
33、证明:∵AE=BF,∴AE+EF=BF+EF 1分
即AF=BE 又∵AC∥BD, 2分
∴∠A=∠B ∵AC=BD
∴△ACF≌△BDE 4分
∴CF=DE 5分
六、(本题满分9分)
34、(1)解:∵AD切⊙O于D,AE=2,EB=6,
∴AD2=AE·AB=2×(2+6)=16
∴AD=4 2分
(2)无论点A在EP上怎么移动(点A不与点E重合),总有AD/AH=ED/FH 3分
证法一:连结DB,交FH于G
解这个方程组得
x=350,y=150 4分
答:年利率是5%和4%的两种储蓄分别存了350元和150元。 5分
解法二:设年利率是5%的储蓄存了x元,则年利率是4%的储蓄了(500-x)元
依题意,得x×5%+(500-X)×4%=23.5 3分
解这个方程,得x=350 ∴500-x=150 4分
答:年利率是5%和4%的两种储蓄分别存了350元和150元。 5分
五、(本题满分5分)
33、证明:∵AE=BF,∴AE+EF=BF+EF 1分
即AF=BE 又∵AC∥BD, 2分
∴∠A=∠B ∵AC=BD
∴△ACF≌△BDE 4分
∴CF=DE 5分
六、(本题满分9分)
34、(1)解:∵AD切⊙O于D,AE=2,EB=6,
∴AD2=AE·AB=2×(2+6)=16
∴AD=4 2分
(2)无论点A在EP上怎么移动(点A不与点E重合),总有AD/AH=ED/FH 3分
证法一:连结DB,交FH于G
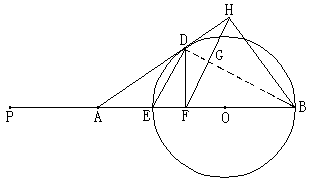 ∵AH是⊙O的切线,∴∠HDB=∠DEB
又∵BH⊥AH,BE为直径,
∴∠BDE=90°
有∠DBE=90°-∠HDB
=∠DBH
在△DFB和△DHB中,DF⊥AB,∠DFB=∠DBH=90°
∴△DFB≌△DHB 4分
∴BH=BF ∴△BHF是等腰三角形
∴BG⊥FH,即BD⊥FH
∴ED∥FH,∴AD/AH=ED/FH 5分
证法二:连结DB
∵AH是⊙O的切线,∴∠HDB=∠DEB
又∵BH⊥AH,BE为直径,
∴∠BDE=90°
有∠DBE=90°-∠HDB
=∠DBH
在△DFB和△DHB中,DF⊥AB,∠DFB=∠DBH=90°
∴△DFB≌△DHB 4分
∴BH=BF ∴△BHF是等腰三角形
∴BG⊥FH,即BD⊥FH
∴ED∥FH,∴AD/AH=ED/FH 5分
证法二:连结DB
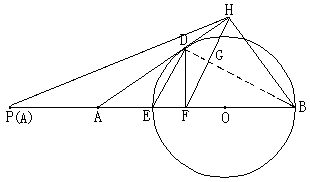 ∵AH是⊙O的切线,∴∠HDB=∠DEF
又∵DF⊥AB,BH⊥DH,∴∠EDF=∠DBH 4分
以BD为直径作一个圆,则此圆必过F、H两点
∴∠DBH=∠DFH,∴∠EDF=∠DFH
∴ED∥FH
∴AD/AH=ED/FH 5分
②∵ED=x,BH=y,BE=6,BF=BH
∴EF=6-y
又∵DF是Rt△BDE斜边上的高,
∴△DFE∽△BDE,∴EF/ED=ED/EB
即ED2=EF·EB ∴x2=6(6-y),即y=-1/6x2=6 7分
∵点A不与点E重合,∴ED=x>0,当A从E向左移动,ED逐渐增大,当A和P重合时,
ED最大,这时,连接OD,则OD⊥PH,∴OD∥BH
又PO=PE+EO=6=3=9,PB=12,OD/BH=PO/PB,BH=OD·PB/PO=4
∴BF=BH=4,EF=EB-BF=6-4=2
由ED2=EF·EF,得:x2=2×6=12
∵x>0,∴x=
∵AH是⊙O的切线,∴∠HDB=∠DEF
又∵DF⊥AB,BH⊥DH,∴∠EDF=∠DBH 4分
以BD为直径作一个圆,则此圆必过F、H两点
∴∠DBH=∠DFH,∴∠EDF=∠DFH
∴ED∥FH
∴AD/AH=ED/FH 5分
②∵ED=x,BH=y,BE=6,BF=BH
∴EF=6-y
又∵DF是Rt△BDE斜边上的高,
∴△DFE∽△BDE,∴EF/ED=ED/EB
即ED2=EF·EB ∴x2=6(6-y),即y=-1/6x2=6 7分
∵点A不与点E重合,∴ED=x>0,当A从E向左移动,ED逐渐增大,当A和P重合时,
ED最大,这时,连接OD,则OD⊥PH,∴OD∥BH
又PO=PE+EO=6=3=9,PB=12,OD/BH=PO/PB,BH=OD·PB/PO=4
∴BF=BH=4,EF=EB-BF=6-4=2
由ED2=EF·EF,得:x2=2×6=12
∵x>0,∴x=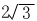 ∴0<x≤
∴0<x≤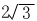 (或由BH=4=y,代入y=-1/6x2+6,得x=
(或由BH=4=y,代入y=-1/6x2+6,得x=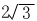 )
故所求函数关系式为y=1/6x2+6 (x<x≤
)
故所求函数关系式为y=1/6x2+6 (x<x≤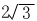 = 9分
= 9分
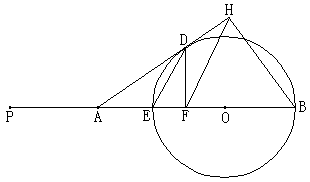
A作⊙O的切线AD,切点为D。过D作DF⊥AB于F,过B作AD的垂线BH,交AD的延长线于H。连结ED
和FH。 (1)若AE=2,求AD的长; (2)当点A在EP上移动(点A不与点E重合)时, ①是否总有AD/AH=ED/FH?试证明你的结论; ②设ED=x,BH=y,求y与x的函数关系式,并写出自变量x的取值范围。
1999年初中毕业会考数学试卷答案和评分标准 说明: 一、《答案》中各行右端所注分数表示正确作完该步应得的累加分数,全卷满分100分 二、《答案》中解法只是该题解法中的一种或几种,如果老先生的解法和本《答案》不同, 可参照《答案》中评分标准的精神,进行评分。 三、评卷时,要坚持每题评阅到底,勿因考生解答中出现错误而中断本题评阅,如果老先 生的解答在某一步出现错误,影响后继部分而未改变本题的内容与难度者,视影响程 度来决定后面部分的得分,但原则上不超过后面部分应得分数的一半,如果有严重概 念性错误,就不给分。 一、填空题(本题满分36分,每小题2分) 1、-3/5,6 2、5.7×105 3、-1,1/2 4、A(1-B)(1+B) 5、80° 6、x≤2
7、6 8、70,2 9、-2a2+a-1 10、相交 11、8 12、-9/4
元5角,两种储蓄各存了多少钱?
 6.函数y=x+
6.函数y=x+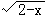 中,自变量x的取值范围是____。
7.已知线段a=4cm,b=9cm,则线段a、b的比例中项是c=____cm。
8.已知线段68,69,70,71,72的平均数是____,方差是____。
9.化简:a(a-1)2-(a+1)(a2-a+1)=____。
10.已知:两圆⊙O1与⊙O2的圆心距O1O2=5cm,两圆半径分别为R1=6cm和R2=8cm,则这两圆的位
中,自变量x的取值范围是____。
7.已知线段a=4cm,b=9cm,则线段a、b的比例中项是c=____cm。
8.已知线段68,69,70,71,72的平均数是____,方差是____。
9.化简:a(a-1)2-(a+1)(a2-a+1)=____。
10.已知:两圆⊙O1与⊙O2的圆心距O1O2=5cm,两圆半径分别为R1=6cm和R2=8cm,则这两圆的位
置关系是____。
11.一个n边形的内解和是1080°,则n=____。
12.关于x的一元二次方程kx2+3x-1=0有两个相等的实数根,则k=____。
13.如图,AB是半圆直径,∠ABC=63°,则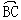 所对的圆周角度数是____。
所对的圆周角度数是____。
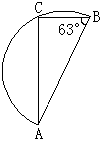 14.计算:
14.计算: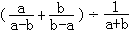 =__________。
15.计算:
=__________。
15.计算: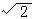 sin45°-sin30°cos60°-tg45°=__________。
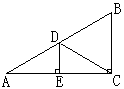
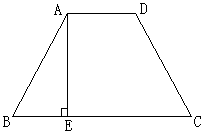
16.下图是屋架设计图一的部分,其中BC⊥AC,DE⊥AC,点D是AB的中点,∠A=30°,AB=7.4m,
sin45°-sin30°cos60°-tg45°=__________。
16.下图是屋架设计图一的部分,其中BC⊥AC,DE⊥AC,点D是AB的中点,∠A=30°,AB=7.4m,
则BC=____m,DE=____m。
 17.甲队有32人,乙队有28人,现在从乙队抽调x人到甲队,使甲队人数是乙队人数的2倍,依题
17.甲队有32人,乙队有28人,现在从乙队抽调x人到甲队,使甲队人数是乙队人数的2倍,依题
意,列出的方程是________________。
18.已知扇形的圆心角是150°,弧长为20π厘米,则这个扇形的半径为____厘米。
二、选择题(本题共10个小题,每小题3分,满分30分)
19.下列计算,正确的是
A.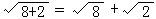 B.
B.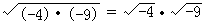
C.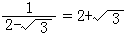 D.
D.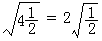 20.下列说法中,正确的是
A.一条射线把一个角分成两个角,这条射线叫做这个角的平分线。
B.P是直线l外一点,A.B.C分别是l上的三点,已知PA=1,PB=2,PC=3,则点P到l的距
20.下列说法中,正确的是
A.一条射线把一个角分成两个角,这条射线叫做这个角的平分线。
B.P是直线l外一点,A.B.C分别是l上的三点,已知PA=1,PB=2,PC=3,则点P到l的距
离一定是1。
C.相等的角是对顶角。
D.钝角的补角一定是锐角。
21.化简(-2a)3b4 ÷ 12a3b2的结果是
A.1/6b2 B.-1/6b2 C.-2/3b2 D.-2/3ab2
22.点P(-2,-4)关于x轴对称的点p'的坐标是
A.(-2,4) B.(2,-4) C.(2,4) D.(-4,-2)
23.下列命题中,真命题是
A.对角线互相平分的四边形是平行四边形
B.对角线相等的四边形是矩形
C.对角线互相垂直的四边形是菱形
D.对角线相等且互相垂直的四边形是正方形
24.已知x<2,化简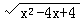 的结果是
A.x-2 B.2-x C.-x-2 D.x+2
25.计算2×(-3)2+(-2)-1÷1/4+3.140的结果为
A.-18 B.-15 C.17 D.21
26.抛物线y=2(x-3)+5的对称轴和顶点坐标分别为
A.x=-3,(-3,5) B.x=3,(3,5)
的结果是
A.x-2 B.2-x C.-x-2 D.x+2
25.计算2×(-3)2+(-2)-1÷1/4+3.140的结果为
A.-18 B.-15 C.17 D.21
26.抛物线y=2(x-3)+5的对称轴和顶点坐标分别为
A.x=-3,(-3,5) B.x=3,(3,5)
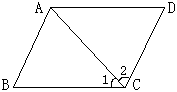
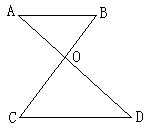
C.x=3,(-3,-5) D.x=-3,(3,-5) 27.已知:如图,AB∥CD,AD与BC相交于O,则下列比例式中,正确的是
|
A.AB/CD=OA/AD B.OA/OD=OB/BC C.AB/CD=OB/OC D.BC/AD=OB/OD |
 |
28.分式方程1/(x+2)+4x/(x2-4)+2/(2-x)=1的根为 A.x1=1,x2=2 B.x1=-1,x2=-2
C.x=2 D.x=1
三、(本题共3个小题,每小题5分,满分15分)
29.解不等式x-2≥(3x-5)/4,并把它的解集在数轴上表示出来。
30.已知函数y=k/(x+1),且当x=-2时,y=-3。
(1)求k的值;
(2)当x=1/2时,求y的值。
31.已知:如图,梯形ABCD中,AD∥BC,AB=DC,AD=2cm,中位线长5cm,高AE=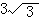 cm,求这
cm,求这
个梯形的腰长。
15、已知实数a、b、c在数轴上的位置如图所示,化简∣a+b∣―∣c―b∣

0
14、(―2)3―∣―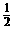 ∣+(
∣+(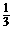 )―2×(1―
)―2×(1―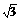 )0
)0
13、(―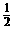 )2―2+2―1×(
)2―2+2―1×(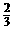 ―∣
―∣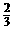 ―2∣)
―2∣)
12、33+(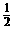 )―2―∣0―1∣+(
)―2―∣0―1∣+(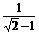 )0
)0
11、三个数3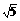 ,2
,2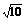 ,
,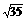 中,最小的一个是
中,最小的一个是
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com