3.小明要在坡度为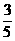的山坡上植树，要想保证水平株距为5 m，则相邻两株树植树地点的高度差应为_____m.

2.在△ABC中,∠C=90°，BC=3，AB=4.则∠B的正弦值是_____.

1.图1表示甲、乙两山坡情况,其中tanα_____tanβ,_____坡更陡.(前一空填“>”“<”或“=”,后一空填“甲”“乙”)

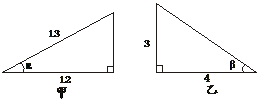
图1

21.(10分)(1)如图6中①、②，锐角的正弦值和余弦值都是随着锐角的确定而确定，变化而变化，试探索随着锐角度数的增大，它的正弦值及余弦值的变化规律.

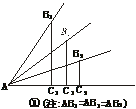
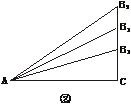
图6

(2)根据你探索到的规律，试分别比较18°、34°、50°、62°、88°这些锐角的正弦值的大小和余弦值的大小.

20.(9分)如图5，某货船以20海里/小时的速度将一批重要的物资由A处运往正西方向的B处，经16小时的航行到达，到达后便接到气象部门通知，一台风中心正由A向北偏西60°方向移动，距台风中心200海里的圆形区域(包括边界)均会受到影响.在B处的货船是否会受到台风的侵袭？说明理由.

19.(9分)“郑集中学”有一块三角形形状的花圃ABC，现可直接测量到∠A=30°，AC= 40 m，BC=25 m，请求出这块花圃的面积.

18.(8分)已知△ABC中，∠C=90°，AC=m，∠BAC=α(如图4),求△ABC的面积.(用α的三角函数及m表示)

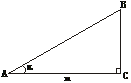
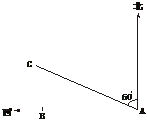
图4　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 图5

17.(16分)计算或化简：

(1)sin45°·cos60°－cos45°·sin30°;

(2)5tan30°－2(cos60°－sin60°).

(3)(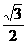tan30°)²⁰⁰⁵·(2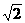sin45°)²⁰⁰⁴;

(4)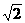(2cos45°－tan45°)－(tan60°+sin30°)⁰－(2sin45°－1)^－1.

16.某人沿着坡度为1∶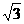的山坡前进了1000 m，则这个人所在的位置升高了

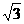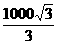A.1000 m　　　　　 　B.500 m　　　　　 　C.500 m　　 　D. m

15.若等腰三角形腰长为4，面积是4，则这个等腰三角形顶角的度数为

A.30°　　　　　 　　　　　　　 B.30°或150°　　 C.60°　　　　　 　D.60°或120°