
题目列表(包括答案和解析)
3. 去年,浙江省国民生产总值达到13340亿元,这个数用科学记数法可表示为(▲)
A. 13.34×104亿元 B. 1.334×104亿元
C. 0.1334×105亿元 D. 1.334×105亿元
2. 方程2x+3=7的解是(▲)
A. x=2 B. x=-2 C. x=1 D. x=-1
1.-3的相反数是(▲)
A. 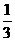 B. -3
C. -
B. -3
C. -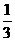 D. 3
D. 3
5. 抛物线y=x2-2(k-1)x-1-k与x轴交于A(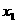 ,0)B(
,0)B(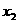 ,0),
,0),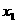 < 0 <
< 0 <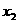 ,与y轴交于C,且
,与y轴交于C,且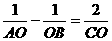 ,问:是否存在直线y=
,问:是否存在直线y=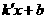 与抛物线交于P,Q,使y轴平分ΔCPQ的面积?若存在,求
与抛物线交于P,Q,使y轴平分ΔCPQ的面积?若存在,求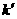 ,b所满足的条件;若不存在,请说明理由.
,b所满足的条件;若不存在,请说明理由.
请做完之后,再看答案
4. ΔABC中,∠C=90º,AC=6,BC=8,M为BC中点,P是AB上一个动点(可与A、B重合),若∠MPD=90º,PD交BC(或 其延长线)于D,设BP=x,y= ,问:是否存在这样的点P,使得ΔMPD∽ΔABC?若存在,求x的值;否则,请说明理由。
,问:是否存在这样的点P,使得ΔMPD∽ΔABC?若存在,求x的值;否则,请说明理由。
3. 抛物线y=ax2+bx+c(a≠0) 图像的最高点的纵坐标是1,试化简代数式|a|+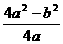
2. 设抛物线y=-3x2-2kx+k2与双曲线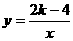 在第二象限中一个交点的横坐标为-2,求k的值以及两图像交点的个数。
在第二象限中一个交点的横坐标为-2,求k的值以及两图像交点的个数。
1. 已知抛物线y=ax2+bx+c与y轴交于点(0,2),与x轴两交点的横坐标之和比它们的积的8倍小1,求a的取值范围。
4. 二次函数在实际问题中的应用,首先是合理、正确的建模,随后才是求解。
[典型例题]
例1. 已知a、b、c为实数,4a-4b+c>0,a+2b+c<0,试比较b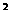 与ac的大小
与ac的大小
解析:已知条件使人联想到二次函数模型中,自变量取两个不同的值所对应的函数值的结构特征,故构造二次函数求解即可。
设y=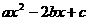
则①a=0时,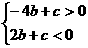 ∴
∴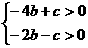 ∴-6b>0 ∴b<0
∴-6b>0 ∴b<0
又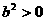 ac=0 ∴
ac=0 ∴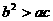
②a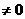 时,当x=2时
时,当x=2时 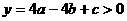 ;当x=-1时,
;当x=-1时,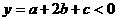
∴抛物线与x轴定有两个不同的交点 。 ∴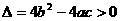 ∴
∴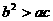
∴由①、②知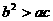
例2. 设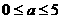 ,且a为实数,3b=a(3a-8),求整数b的个数。
,且a为实数,3b=a(3a-8),求整数b的个数。
解析:只有先求出b的取值范围,才能从这个范围中找出符合题设条件的整数b有几个。
∵3b=a(3a-8)=3a(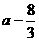 ) (
) (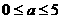 )
)
∴这是一个开口向上,顶点为(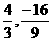 )的抛物线模形
)的抛物线模形
又a=5时,b=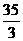 ∴当
∴当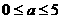 时,
时,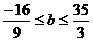
∴整数b=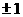 、0、2、3、4…、11共计有13个。
、0、2、3、4…、11共计有13个。
例3. (如图)ΔABC中,∠C=90º,AC=BC=3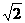 ,动点P在AB上,过P作PE⊥AC于E,PF⊥BC于F,设CF=x,问:是否存在这样的点P,使RtΔAEP,RtΔPFB以及矩形ECFP的面积都小于4?
,动点P在AB上,过P作PE⊥AC于E,PF⊥BC于F,设CF=x,问:是否存在这样的点P,使RtΔAEP,RtΔPFB以及矩形ECFP的面积都小于4?
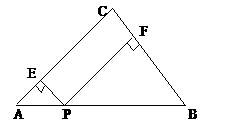
解:由题意,可得S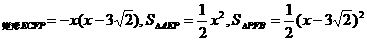 ,不妨分别设为y1,y2和y3
,不妨分别设为y1,y2和y3
解y1,y2组成的方程组,得交点O(0,0),A(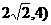
解y2,y3组成的方程组,得交点B(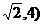 ,C(
,C(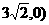
据此,画出草图,从图中不难看出0≤x≤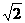 时,y3≥4;
时,y3≥4;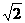 <x≤
<x≤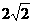 时,y1≥4;
时,y1≥4;
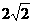 ≤x<
≤x<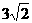 时,y2≥4
时,y2≥4
∴综上所知,当0<x<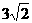 时,y1,y2,y3的最大值不都小于4;
时,y1,y2,y3的最大值不都小于4;
∴不存在这样的点P,使满足题设的条件。
[模拟试题](答题时间:30分钟)
3. 体会在二次函数的学习中,对图像与性质的研究渗透了数形结合思想;求解析式时应用了待定系数法和配方法;在实际问题的求解中应用了分类讨论法等数学思想和方法。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com