17．解析：在0°到360°范围内，由几何方法可求得α=60°.

∴A={α|α=60°+k·360°，k∈Z}

其中最大的负角为－300°(当k=－1时)

绝对值最小的角为60°(当k=0时)

13．第二或第四象限，第一或第二象限或终边在y轴的正半轴上　 14．30°　 1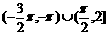5．　 16．25　

1．D 2．A3．B4．D5．D6．B7．C 8．B9．B10．A11．C12．C

22．有两种正多边形，其中一正多边形的一内角的度数与另一正多边形的一内角的弧度数之比为144∶π，求适合条件的正多边形的边数

21．已知集合A={，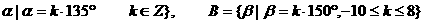

　　 求与A∩B中角终边相同角的集合S.

20．自行车大链轮有48个齿，小链轮有20个齿，彼此由链条连接，当大链轮转过一周时，小链轮转过的角度是多少度？多少弧度?？

19．已知一扇形的周长为c(c＞0)，当扇形的弧长为何值时，它有最大面积？并求出面积的最大值.

18．已知△ABC的三内角A、B、C成等差数列，且A－C=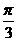，求cos²A+cos²B+cos²C的值.

17．如果角α的终边经过点M(1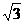，)，试写出角α的集合A，并求集合A中最大的负角和绝对值最小的角.

16．已知扇形的周长为20 cm，当扇形的中心角为多大时，它有最大面积，最大面积是