
题目列表(包括答案和解析)
16、解: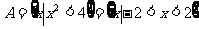 ,…………………………………… 2分
,…………………………………… 2分
 ,……………………… 4分
,……………………… 4分
(1)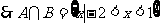 ;……………………………………………………. 6分
;……………………………………………………. 6分
(2)因为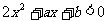 的解集为
的解集为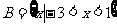 ,
,
所以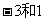 为
为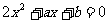 的两根,……………………………………… 8分
的两根,……………………………………… 8分
故 ,所以
,所以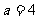 ,
,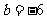 .……………………………………. 10分
.……………………………………. 10分
17解析:(1) ………. 2分
………. 2分
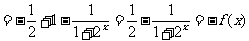 ………. 4分
………. 4分
又函数f(x)的定义域为R,故函数f(x)为奇函数. ………. 5分
(2)证明:令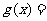 x f(x)由(1)易知函数g(x)为偶函数,………. 6分
x f(x)由(1)易知函数g(x)为偶函数,………. 6分
当x>0时,由指数函数的单调性可知: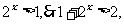 ………. 7分
………. 7分
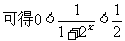 ,
,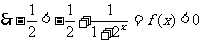 ,故x>0时有x f(x)<0. …. 8分
,故x>0时有x f(x)<0. …. 8分
又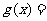 x f(x)是偶函数,当x<0时,-x>0,∴当x<0时g(x)=g(-x)<0,即对于x≠0的任何实数x,均有x f(x)<0. ………. 10分
x f(x)是偶函数,当x<0时,-x>0,∴当x<0时g(x)=g(-x)<0,即对于x≠0的任何实数x,均有x f(x)<0. ………. 10分
6.D 7、B 8、A 9、C 10、B
11答案: 12答案:
12答案: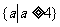 13 答案:
13 答案: 14答案:a=.
14答案:a=.
15解析:(1)方法一: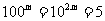 ,……… 2分
,……… 2分
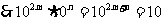 ,……… 4分
,……… 4分
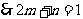 ……… 5分
……… 5分
方法二: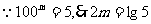 ,……… 2分
,……… 2分
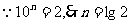 ,……… 3分
,……… 3分
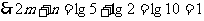 ……… 5分
……… 5分
(2)由(1)可知f(x1x2…x2010)=f(x1)+f(x2)+…+f(2010)=1,……… 7分
∴f(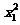 )+f(
)+f(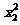 )+…+f(
)+…+f(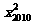 )=2[f(x1)+f(x2)+…+f(x2010)] ……… 9分
)=2[f(x1)+f(x2)+…+f(x2010)] ……… 9分
=2×1=2. ……… 10分
1、B 2、C 3、 A 4 、B 5、 D
22.(本小题满分14分)
已知函数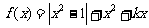 ,且定义域为(0,2).
,且定义域为(0,2).
(1)求关于x的方程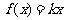 +3在(0,2)上的解;
+3在(0,2)上的解;
(2)若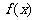 是定义域(0,2)上的单调函数,求实数
是定义域(0,2)上的单调函数,求实数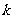 的取值范围;
的取值范围;
(3)若关于x的方程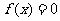 在(0,2)上有两个不同的解
在(0,2)上有两个不同的解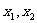 ,求k的取值范围。
,求k的取值范围。
广东实验中学2010-2011学年(上)高一期中考试评分标准
21.(本小题满分13分)
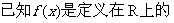 单调函数,
单调函数,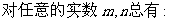
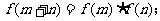
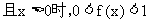 .
.
(1)证明:f(0)=1且x<0时f(x)>1;
(2)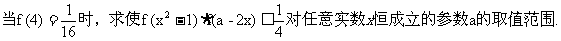
20.(本小题13分)已知二次函数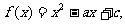 (其中
(其中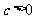 )
)
(1)试讨论函数 的奇偶性.
的奇偶性.
(2)当 为偶函数时,若函数
为偶函数时,若函数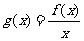 ,试证明:函数
,试证明:函数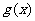 在
在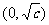 上单调递减,在
上单调递减,在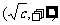 上单调递增;
上单调递增;
19.若关于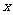 的方程
的方程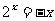 ,
,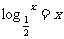 ,
,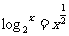 的解分别为
的解分别为 ,则
,则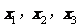 的大小关系是_____>______>_____.
的大小关系是_____>______>_____.
18.若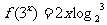 ,则
,则 ____________.
____________.
17.(本小题10分)已知函数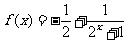
(1) 证明:函数f(x)是奇函数. (2) 证明:对于任意的非零实数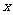 恒有x f(x)<0成立.
恒有x f(x)<0成立.
16.(本小题10分)设集合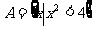 ,
,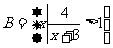 .
.
(1)求集合 ;
;
(2)若不等式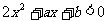 的解集为
的解集为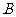 ,求
,求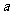 ,
,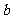 的值.
的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com