
题目列表(包括答案和解析)
4、方程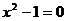 的解集用列举法表示为( )
的解集用列举法表示为( )
A.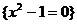 B.
B. 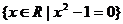 C.
C. 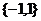 D. 以上都不对
D. 以上都不对
3、下列函数中,在区间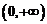 上是增函数的是( )
上是增函数的是( )
A .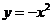 B .
B .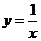 C.
C. 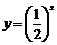 D.
D. 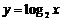
2.设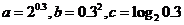 ,则
,则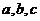 的大小关系是( )
的大小关系是( )
A.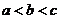 B.
B.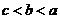 C.
C.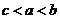 D.
D.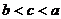
1.已知全集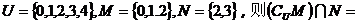 ( )
( )
A. 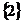 B.
B. 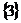 C.
C.
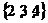 D.
D.
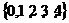
21.(本小题满10分)注意:第(3)小题平行班学生不必做,特保班学生必须做。
对于函数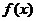 ,若存在x0∈R,使
,若存在x0∈R,使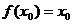 成立,则称x0为
成立,则称x0为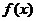 的不动点。
的不动点。
已知函数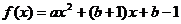 (a≠0)。
(a≠0)。
(1)当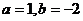 时,求函数
时,求函数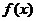 的不动点;
的不动点;
(2)若对任意实数b,函数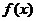 恒有两个相异的不动点,求a的取值范围;
恒有两个相异的不动点,求a的取值范围;
(3)(特保班做) 在(2)的条件下,若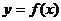 图象上A、B两点的横坐标是函数
图象上A、B两点的横坐标是函数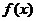 的不动点,且A、B两点关于点
的不动点,且A、B两点关于点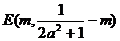 对称,求
对称,求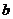 的的最小值。
的的最小值。
三明一中2010-2011年度上学期学段考
20.(本小题满分10分)已知函数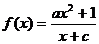 是奇函数,且
是奇函数,且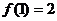
(1)求函数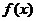 的解析式;
的解析式;
(2)当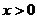 时,讨论函数
时,讨论函数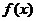 的单调性。
的单调性。
19.(本小题满分10分)
某车间生产一种仪器的固定成本是10000元,每生产一台该仪器需要增加投入100元,已知总收益满足函数: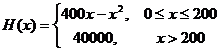 ,其中
,其中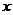 是仪器的月产量。
是仪器的月产量。
(1)将利润表示为月产量的函数(用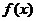 表示);
表示);
(2)当月产量为何值时,车间所获利润最大?最大利润是多少元?
(总收益=总成本+利润)
18.(本小题满分9分)
以下是用二分法求方程 的一个近似解(精确度为0.1)的不完整的过程,请补充完整。
的一个近似解(精确度为0.1)的不完整的过程,请补充完整。
|
区间 |
中点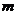 |
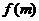 符号 符号 |
区间长度 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
解:设函数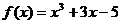 ,
,
其图象在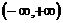 上是连续不
上是连续不
断的,且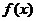 在
在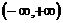 上是
上是
单调递______(增或减)。
先求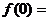 _______,
_______,
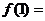 ______,
______,
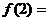 ____________。
____________。
所以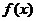 在区间____________内存在零点
在区间____________内存在零点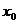 ,再填上表:
,再填上表:
下结论:_______________________________。
(可参考条件: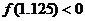 ,
,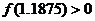 ;符号填+、-)
;符号填+、-)
17.(本小题满分9分)
已知R为全集,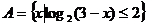 ,
,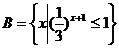 ,求(
,求(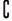 RA)
RA)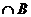
16.给出下列四个命题:
(1)函数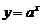 (
(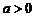 且
且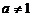 )与函数
)与函数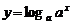 (
(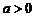 且
且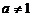 )的定义域相同;
)的定义域相同;
(2)函数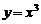 与
与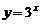 的值域相同;
的值域相同;
(3)函数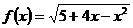 的单调递增区间为
的单调递增区间为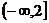 ;
;
(4)函数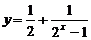 与
与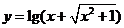 都是奇函数。
都是奇函数。
其中正确命题的序号是__________(把你认为正确的命题序号都填上)。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com