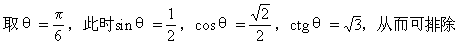
B、C、D，应选A．

[说明]　 此例题用多种方法求解选项，指出3种选择题的技巧．

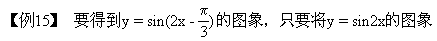
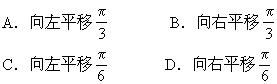
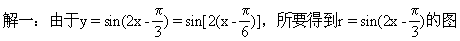
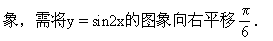
∴应选D

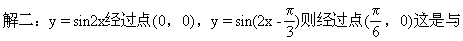
x轴交点中在原点右边最接近原点的交点，而在原点左边与x轴交点中最

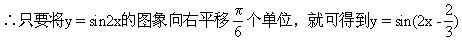
的图象．

∴选D

[说明]　 y=Asin(ωx+j)(A＞0，ω＞0)x∈R的图象可由y=sinx的图象经下列各种顺序变换得到的．

(1)先平移，后伸缩：

①把y=sinx的图象向左(j＞0)或向右(j＜0)沿x轴方向平移|j|个单位；(相位变换)

(周期变换)

③把所有各点纵坐标伸长(A＞1)或缩短(0＜A＜1)到原来的A倍，横坐标不变(振幅变换)

(2)先伸缩，后平移

①把y=sinx图象上各点的横坐标缩短(ω＞1)或伸长(0＜ω＜1)到原

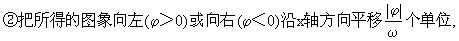
(相位变换)

③把所有各点纵坐标伸长(A＞1)或缩短(0＜A＜1)到原来的A倍横坐标不变(振幅变换)

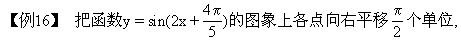
再把横坐标缩小到原来的一半，纵坐标扩大到原来的4倍，则所得的图象的解析式是　　 [　　 ]

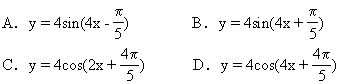
∴选A．

[例17]　 方程sin2x=sinx在区间(0，2π)内解的个数是

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 [　　 ]

A．1　　　　　 B．2　　　　　　 C．3　　　　　　　 D．4

[分析]　 本题有两类解法

(1)求出方程在(0，2π)内的所有解，再数其解的个数．而决定选项，对于选择题，此法一般不用．

(2)在同一坐标系中作出函数y=sin2x和y=sinx的图象，如图2-18所示．

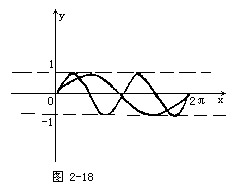
它们在(0，2π)内交点个数，即为所求方程解的个数，从而应选C．

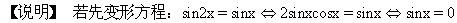
它体现了数、形的结合．

[例18]　 设函数f(x)是定义在R上的周期为3的奇函数，且f(1)=2，则f(5)=____

解：∵f(x)是奇函数，且f(1)=2，∴f(-1)=-2

又∵f(x)是周期为3的函数．　 ∴f(3+x)=f(x)

∴f(-1+3)=f(-1)=-2　 即f(2)=-2

f(2+3)=f(2)=-2　 即f(5)=-2

[例19]　 有一块扇形铁板，半径为R，圆心角为60°，从这个扇形中切割下一个内接矩形，即矩形的各个顶点都在扇形的半径或弧上，求这个内接矩形的最大面积．

[分析]　 本题入手要解决好两个问题．

(1)内接矩形的放置有两种情况，如图2-19所示，应该分别予以处理．

(2)求最大值问题这里应构造函数，怎么选择便于以此表达矩形面积的自变量．

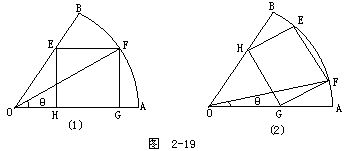
解：如图2-19(1)设∠FOA=θ，则FG＝Rsinθ

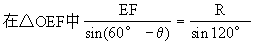
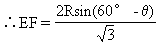
又设矩形EFGH的面积为S，那么

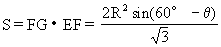
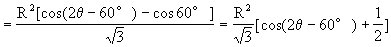
又∵0°＜θ＜60°，故当cos(2θ－60°)＝1，即θ=30′时，

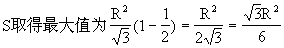
如图2-19 (2)，设∠FOA＝θ，则EF＝2Rsin(30°-θ)，在△OFG中，∠OGF＝150°

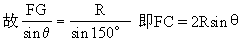
设矩形的面积为S．

那么S＝EFFG＝4R²sinθsin(30°-θ)

＝2R²［cos(2θ-30°)－cos30°]

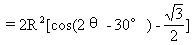
又∵0＜θ＜30°，故当cos(2θ-30°)＝1

作出三角函数线，如图2-17

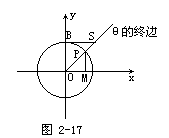
MP=sinθ，OM=cosθ，BS=ctgθ

通过观察和度量得MP＜OM＜BS

从而有sinθ＜cosθ＜ctgθ

∴应选A

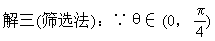
∴cosθ＞sinθ

从而可剔除B、D．

再由sinθ＜ctgθ，故可剔除C

故选A

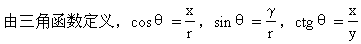
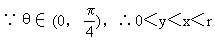
故选A．

3．要掌握对数列各项的同加、同减、同乘以某一个不等于零的数的变形方法，将其转化为常见的一些数列．

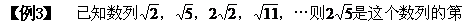
几项．

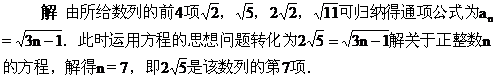
[例4]　 已知下面各数列{a_n}的前n项和S_n的公式，求数列的通项公式．

(1)S_n＝2n²－3n　 (2)S_n＝n²+1

(3)S_n＝2ⁿ+3　　　 　(4)S_n＝(－1)ⁿ⁺¹·n

解　 (1)当n=1时，a₁=S₁＝－1；

当n≥2时，a_n＝S_n－S_n-1=(2n²－3n)－[2(n－1)²－3(n－1)]＝4n－5，由于a₁也适合此等式，因此a_n=4n－5．

(2)当n＝1时，a₁＝S₁=1+1＝2；

当n≥2时，a_n＝S_n－S_n-1=n²+1－[(n－1)²+1]＝2n－1，由于a₁不适合于此等式，

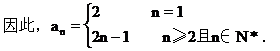
(3)当n＝1时，a₁=S₁＝2+3=5；

当n≥2时，a_n=S_n－S_n-1＝2ⁿ+3－(2^n-1+3)＝2^n-1，由于a₁不适合于此等式，

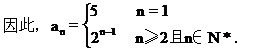
(4)当n＝1时，a₁＝S₁=(－1)²·1=1；

当n≥2时，a_n＝S_n－S_n-1=(－1)ⁿ⁺¹·n－(－1)ⁿ·(n－1)=(－1)ⁿ⁺¹(2n－1)，由于a₁也适可于此等式，因此a_n＝(－1)ⁿ⁺¹(2n－1)，n∈N*．

说明　 已知S_n求a_n时，要先分n＝1和n≥2两种情况分别进行计算，然后验证能否统一．

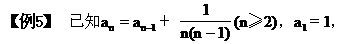
(1)写出数列的前5项；

(2)求a_n．

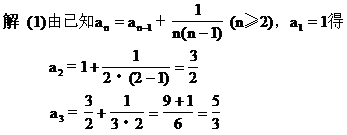
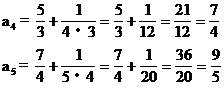
(2)由第(1)小题中前5项不难求出．

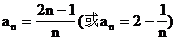
[例6]　 数列{a_n}中，a₁＝1，对所有的n≥2，都有a₁·a₂·a₃·…·a_n＝n²．

(1)求a₃+a₅；

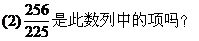
解　 由已知：a₁·a₂·a₃·…·a_n＝n²得

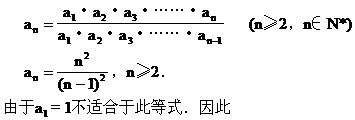
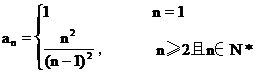
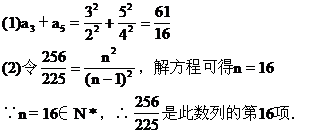
说明　 (1)“知和求差”、“知积求商”是数列中常用的基本方法．

(2)运用方程思想求n，若n∈N*，则n是此数列中的项，反之，则不是此数列中的项．

[例7]　 已知数a_n=(a²－1)(n³－2n)(a=≠±1)是递增数列，试确定a的取值范围．

解法一　 ∵数列{a_n}是递增数列，∴a_n+1＞a_n

a_n+1－a_n＝(a²－1)[(n+1)³－2(n+1)]－(a²－1)(n³－2n)

＝(a²－1)[(n+1)³－2(n+1)－n³+2n]

＝(a²－1)(3n²+3n－1)

∵(a²－1)(3n²+3n－1)＞0

又∵n∈N*，∴3n²+3n－1=3n(n+1)－1＞0

∴a²－1＞0，解得a＜－1或a＞1．

解法二　 ∵{a_n}是递增数列，∴a₁＜a₂即：

(a²－1)(1－2)＜(a²－1)(8－4)

化简得　 a²－1＞0

∴a＜－1或a＞1

说明　 本题从函数的观点出发，利用递增数列这一已知条件，将求取值范围的问题转化为解不等式的问题

2．对于常见的一些数列的通项公式(如：自然数列，a_n=n；自然数的平方数列，a_n＝n²；奇数数列，a_n＝2n－1；偶数数列，a_n=2n；

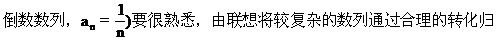
纳出数列的通项公式．

1．用归纳法写出数列的一个通项公式，体现了由特殊到一般的思维规律．对于项的结构比较复杂的数列，可将其分成几个部分分别考虑，然后将它们按运算规律结合起来．

16.(12分)已知集合A=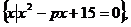

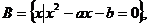
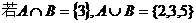，分别求实数p,a ,b 的值。

17(12分)二次函数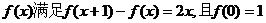

(1)求f(x)的解析式；

(2)在区间[-1，1]上，y= f(x)的图像恒在y=2x+m的图像上方，试确定实数m的取值范围。

18(12分)奇函数f(x)在定义域(-1，1)内是减函数，又f(1-a)+f(1-a²)<0，求a的取值范围。

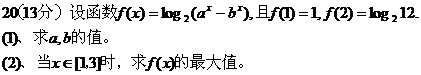
21(13分)已知函数：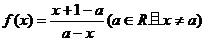

⑴证明：f(x)+2+f(2a－x)=0对定义域内的所有x都成立.

⑵当f(x)的定义域为[a+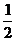,a+1]时，求证：f(x)的值域为[－3，－2]；

⑶设函数g(x)=x²+|(x－a)f(x)| ,求g(x) 的最小值

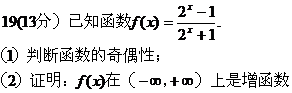
15. 不等式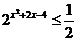的解集为_____________.

14. 水池有两个相同的进水口和一个出水口，每个口进出水速度如图甲、乙所示，某天0点到6点该水池的蓄水量如图丙所示(至少打开一个水口)：

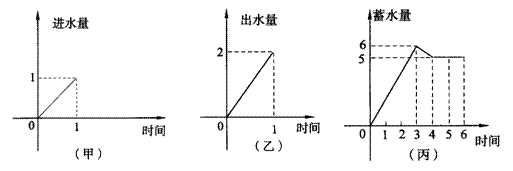
给出以下3个论断：①0点到3点只进水不出水；②3点到4点不进水只出水；③4点到6点不进水也不出水，则一定正确的论断是__________.

13. 1992年底世界人口达到54.8亿,若人口的年平均增长率为1%,经过x年后世界人口数为 y亿,则y与x的函数解析式为_________.