4．对具有线性相关关系的变量x，y，测得一组数据如下表：

根据上表，利用最小二乘法得它们的回归直线方程为 ＝10.5x＋ ，据此模型来预测当x＝20时，y的估计值为(　)

A．210　 　　　　　　　　　　　　　　　　　　　 B．210.5

C．211.5　 　　　　　　　　　　　　　　　　　 D．212.5

解析：由数据可知＝＝5，＝＝54，将(，)代入回归直线方程 ＝10.5x＋ 可得 ＝54－52.5＝1.5，即回归直线方程为 ＝10.5x＋1.5，令x＝20，得 ＝10.5×20＋1.5＝211.5，故选C.

答案：C

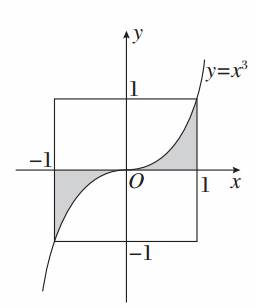
3．[2014·湖北八市调考]如图，设D是图中边长为2的正方形区域，E是函数y＝x³的图象与x轴及x＝±1围成的阴影区域．向D中随机投一点，则该点落入E中的概率为(　)

A.　 　　　　　　　　　　　　　　　　　　　　　 B.

C. 　　　　　　　　　　　　　　　　　　　　　　　 D.

解析：易知区域D的面积为4，由定积分公式知区域E的面积为，因此，点落入E中的概率P＝＝.选B.

答案：B

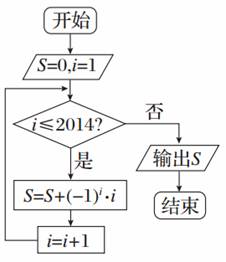
2．执行如图所示的程序框图，输出结果S等于(　)

A．1006　 　　　　　　　　　　　　　　　　　　 B．1007

C．1008　 　　　　　　　　　　　　　　　　　　 D．1009

解析：根据程序框图，S＝(－1＋2)＋(－3＋4)＋…＋(－2013＋2014)＝1007，输出的S为1007.

答案：B

一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的．

1．在某大学数学专业的160名学生中开展一项社会调查，先将学生随机编号为01,02,03，…，160，采用系统抽样的方法抽取样本，已知抽取的学生中最小的两个编号为07号、23号，那么抽取的最大编号应该是(　)

A．150　 　　　　　　　　　　　　　　　　　　　 B．151

C．142　 　　　　　　　　　　　　　　　　　　　 D．143

解析：由最小的两个编号为07,23可知，抽样间距为16，因此抽取人数的比例为，即抽取10名同学，其编号构成首项为07，公差为16的等差数列，故最大编号为7＋9×16＝151.

答案：B

22．(本小题满分12分)已知椭圆C：＋＝1(a>b>0)的左、右焦点分别是F₁、F₂，离心率为，过右焦点F₂的直线l与椭圆C相交于A、B两点，△F₁AB的周长为8.

(1)求椭圆C的方程；

(2)求△F₁AB内切圆半径R的最大值．

解：(1)∵△F₁AB的周长为8，

∴4a＝8，∴a＝2，

又椭圆C的离心率e＝＝，∴c＝，∴b²＝a²－c²＝1.

∴椭圆C的方程为＋y²＝1.

(2)由题设知，直线l不能与x轴重合，故可设直线l的方程为x＝my＋(m∈R)．

由，得(m²＋4)y²＋2my－1＝0.

设A(x₁，y₁)、B(x₂，y₂)，

则y₁＋y₂＝－，y₁y₂＝－，

∴|y₁－y₂|＝

＝＝.

∴△F₁AB的面积S＝|F₁F₂|·|y₁－y₂|＝.

又△F₁AB的面积S＝×8×R，

从而有R＝(m∈R)．

令t＝，则R＝≤＝.

当且仅当t＝，t＝，即m＝±时，等号成立．

∴当m＝±时，R取得最大值.

21．(本小题满分12分)已知椭圆与双曲线x²－y²＝1有相同的焦点，且离心率为.

(1)求椭圆的标准方程；

(2)过点P(0,1)的直线与该椭圆交于A，B两点，O为坐标原点，若＝2，求△AOB的面积．

解：(1)设椭圆方程为＋＝1，a>b>0.

由c＝，可得a＝2，b²＝a²－c²＝2，

故所求方程为＋＝1.

(2)设A(x₁，y₁)，B(x₂，y₂)，

由＝2得，可得x₁＝－2x₂.①

由题意知直线斜率存在，故设直线方程为y＝kx＋1，代入椭圆方程整理，得(2k²＋1)x²＋4kx－2＝0，

则x₁＋x₂＝－，②

x₁x₂＝.③

由①②得，x₂＝，将x₁＝－2x₂代入③得x＝，

所以()²＝，解得k²＝.

又△AOB的面积S＝|OP|·|x₁－x₂|＝·＝＝.

故△AOB的面积是.

20．(本小题满分12分)设抛物线C：y²＝2px(p>0)的焦点为F，直线l过F且与抛物线C交于M，N两点，已知当直线l与x轴垂直时，△OMN的面积为2(O为坐标原点)．

(1)求抛物线C的方程；

(2)是否存在直线l，使得以线段MN为对角线的正方形的第三个顶点恰好在y轴上？若存在，求出直线l的方程；若不存在，请说明理由．

解：(1)∵当直线l与x轴垂直时，|MN|＝2p，∴S_△OMN＝×2p×＝＝2，∴p＝2，

∴抛物线C的方程为y²＝4x.

(2)设正方形的第三个顶点为P，

∵直线l与x轴垂直或y＝0时，不满足条件．

故可设直线l：y＝k(x－1)(k≠0)，M(x₁，y₁)，N(x₂，y₂)，P(0，y₀)．

联立，可得k²x²－(2k²＋4)x＋k²＝0，

则.

∴线段MN的中点为(，)，，

则线段MN的垂直平分线为y－＝－(x－1－)，故P(0，＋)．

又·＝0，∴x₁x₂＋(y₁－y₀)(y₂－y₀)＝0，即x₁x₂＋y₁y₂－y₀(y₁＋y₂)＋y＝0.

1－4－y₀·＋y＝0，化简得，ky－4y₀－3k＝0，由y₀＝＋代入上式化简得，(3k⁴－4)(k²＋1)＝0，解得k＝±.

∴存在直线l：y＝±(x－1)满足题意．

19．(本小题满分12分)[2014·福州八中质检]已知椭圆C：＋＝1(a>b>0)过点M(0，－1)，四个顶点所围成的图形面积为2.直线l：y＝kx＋t与椭圆C相交于A，B两点，且∠AMB＝90°.

(1)求椭圆C的方程；

(2)试判断直线l是否恒过定点？如果是，求出定点坐标；如果不是，请说明理由．

解：(1)由题意得，解得.

∴椭圆C的方程为＋y²＝1.

(2)设A(x₁，y₁)，B(x₂，y₂)．联立椭圆与直线方程，得(1＋2k²)x²＋4ktx＋2t²－2＝0，

∴8(2k²－t²＋1)>0且x₁＋x₂＝－，x₁·x₂＝，

∴y₁·y₂＝(kx₁＋t)(kx₂＋t)＝k²x₁x₂＋kt(x₁＋x₂)＋t²＝＝，

y₁＋y₂＝k(x₁＋x₂)＋2t＝.

∵＝(x₁，y₁＋1)，＝(x₂，y₂＋1)，且∠AMB＝90°，

∴·＝x₁x₂＋(y₁＋1)(y₂＋1)

＝x₁x₂＋y₁y₂＋y₁＋y₂＋1

＝＋＋＋1

＝

＝＝0，

解得t＝或t＝－1(舍去)．∴直线l的方程为y＝kx＋.

∴直线l恒过定点(0，)．

18．(本小题满分12分)已知△ABC的三个顶点为A(0，－3)，B(－1,0)，C(3,0)，直线l：(m＋2)x＋(1－m)y－2m－4＝0(m∈R)．

(1)求△ABC的外接圆M的方程；

(2)证明直线l与圆M相交，并求M被l截得的弦长最短时m的值．

解：(1)设圆M的方程为x²＋y²＋Dx＋Ey＋F＝0，将A，B，C三点的坐标代入方程得，解得.

所以圆M的方程为x²＋y²－2x＋2y－3＝0.

(2)由(1)知圆M的圆心为M(1，－1)，半径r＝.

直线l的方程可化为(x－y－2)m＋2x＋y－4＝0，它必经过直线x－y－2＝0与2x＋y－4＝0的交点．由得，故直线l恒过点N(2,0)．

连接NM，又|NM|＝<，所以点N(2,0)在圆M内，故直线l与圆M恒相交．

结合图形可知：当直线l⊥MN时，M被直线l所截得的弦长最短．

此时k_MN＝＝1，则k_l＝－1，即＝－1，所以m＝－.

三、解答题

17．(本小题满分10分)[2014·石家庄质检]已知动点P到定点A(0,1)的距离比它到定直线y＝－2的距离小1.

(1)求动点P的轨迹C的方程；

(2)已知点Q为直线y＝－1上的动点，过点Q作曲线C的两条切线，切点分别为M，N，求证：M，Q，N三点的横坐标成等差数列．

解：(1)由动点P到定点A(0,1)的距离比它到定直线y＝－2的距离小1，可知动点P到定点A(0,1)的距离等于它到定直线y＝－1的距离，由抛物线的定义可知动点P的轨迹C的方程为x²＝4y.

(2)由题意知y′＝.

设M(x₁，y₁)，N(x₂，y₂)，Q(x₀，－1)，则切线MQ：y－y₁＝(x－x₁)，切线NQ：y－y₂＝(x－x₂)．

因为MQ，NQ交于点Q(x₀，－1)，

所以－1－y₁＝(x₀－x₁)，－1－y₂＝(x₀－x₂)，可得直线MN：－1－y＝(x₀－x)，

又y＝，所以x²－2x₀x－4＝0.易知x₁，x₂为方程x²－2x₀x－4＝0的两个解，

由根与系数的关系可知x₁＋x₂＝2x₀，

所以M，Q，N三点的横坐标成等差数列．