2．若数列{a_n}为等差数列，且a₇＋a₈＋a₉＝12，则a₉－a₁₀＝(　)

A．1　 　　　　　　　　　　　　　　　　　　　　　 B．2

C．3　 　　　　　　　　　　　　　　　　　　　　　 D．4

解析：a₇＋a₉＝2a₈，代入已知得3a₈＝12，所以a₈＝4，a₉－a₁₀＝(2a₉－a₁₀)＝(a₉＋a₉－a₁₀)＝a₈＝2.

答案：B

一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的．

1．已知实数a，b满足ab≠0且a<b，则下列命题成立的是(　)

A．|a|<|b|　 　　　　　　　　　　　　　　　　　 B．a²b<ab²

C.<　 　　　　　　　　　　　　　　　　　 D.<

解析：在a<b两边同时除以a²b²即可得到<.故选C.

答案：C

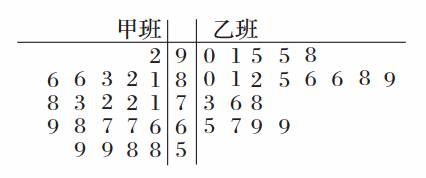
22．(本小题满分12分)某大型歌手选秀活动，过程分为初赛、复赛和决赛．经初赛进入复赛的40名选手被平均分成甲、乙两个班，由组委会聘请两位导师各负责一个班进行声乐培训．右图是根据这40名选手参加复赛时获得的100名大众评审的支持票数制成的茎叶图．赛制规定：参加复赛的40名选手中，获得的支持票数不低于85票的可进入决赛，其中票数不低于95票的选手在决赛时拥有“优先挑战权”．

(1)从进入决赛的选手中随机抽出2名，X表示其中拥有“优先挑战权”的人数，求X的分布列和数学期望；

(2)请填写下面的2×2列联表，并判断能否在犯错误的概率不超过0.025的前提下认为进入决赛与选择的导师有关？

下面的临界值表仅供参考：

(参考公式：K²＝，其中n＝a＋b＋c＋d)

解：(1)由题中茎叶图可知，进入决赛的选手共13名，其中拥有“优先挑战权”的选手共3名．

根据题意，X的可能取值为0,1,2.

P(X＝0)＝＝，P(X＝1)＝＝，P(X＝2)＝＝.

X的分布列如下：

E(X)＝0×＋1×＋2×＝.

(2)由茎叶图可得2×2列联表如下：

K²＝≈5.584>5.024，

因此在犯错误的概率不超过0.025的前提下可以认为进入决赛与选择的导师有关.

21．(本小题满分12分)某班学生在数学校本课程的选课过程中，已知第一小组与第二小组各有6位同学，每位同学都只选了一个科目，且第一小组选《数学运算》的有1位同学，选《数学解题思想与方法》的有5位同学；第二小组选《数学运算》的有2位同学，选《数学解题思想与方法》的有4位同学．现从第一、第二小组中各任选2位同学分析选课情况．

(1)求选出的4位同学均选《数学解题思想与方法》的概率；

(2)设ξ为选出的4位同学中选《数学运算》的人数，求ξ的分布列和数学期望．

解：(1)设“从第一小组选出的2位同学选《数学解题思想与方法》”为事件A，“从第二小组选出的2位同学选《数学解题思想与方法》”为事件B.

由于事件A、B相互独立，且P(A)＝＝，P(B)＝＝.

所以选出的4位同学均选《数学解题思想与方法》的概率为P(AB)＝P(A)·P(B)＝×＝.

(2)ξ的所有可能取值为0、1、2、3，则

P(ξ＝0)＝，P(ξ＝1)＝·＋·＝，

P(ξ＝3)＝·＝，P(ξ＝2)＝1－P(ξ＝0)－P(ξ＝1)－P(ξ＝3)＝.

所以ξ的分布列为

故ξ的数学期望E(ξ)＝0×＋1×＋2×＋3×＝1.

20．(本小题满分12分)为增强市民的节能环保意识，某市面向全市征召义务宣传志愿者．从符合条件的500名志愿者中随机抽取100名志愿者，其年龄频率分布直方图如图所示，其中年龄分组区间是：[20,25)，[25,30)，[30,35)，[35,40)，[40,50]．

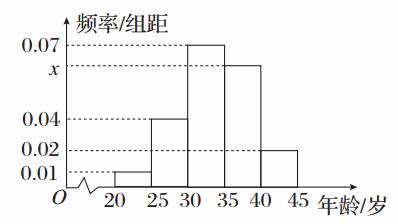
(1)求图中x的值并根据频率分布直方图估计这500名志愿者中年龄在[35,40)岁的人数；

(2)在抽出的100名志愿者中按年龄采用分层抽样的方法抽取20名参加中心广场的宣传活动，再从这20名中采用简单随机抽样方法选取3名志愿者担任主要负责人．记这3名志愿者中“年龄低于35岁”的人数为X，求X的分布列及数学期望．

解：(1)∵小矩形的面积等于频率，

∴除[35,40)外的频率和为0.70，

∴x＝＝0.06.

500名志愿者中，年龄在[35,40)岁的人数为0.06×5×500＝150(人)．

(2)用分层抽样的方法，从中选取20名，则其中年龄“低于35岁”的人有12名，“年龄不低于35岁”的人有8名．

故X的可能取值为0,1,2,3，

P(X＝0)＝＝，

P(X＝1)＝＝，

P(X＝2)＝＝，

P(X＝3)＝＝，

故X的分布列为

所以E(X)＝0×＋1×＋2×＋3×＝.

19．(本小题满分12分)一个袋中装有四个形状大小完全相同的球，球的编号分别为1,2,3,4.

(1)从袋中随机抽取一个球，将其编号记为a，然后从袋中余下的三个球中再随机抽取一个球，将其编号记为b，求关于x的一元二次方程x²＋2ax＋b²＝0有实根的概率；

(2)先从袋中随机抽取一个球，该球的编号记为m，将球放回袋中，然后从袋中随机抽取一个球，该球的编号记为n.若以(m，n)作为点P的坐标，求点P落在区域内的概率．

解：(1)设事件A为“方程x²＋2ax＋b²＝0有实根”．

当a>0，b>0时，方程x²＋2ax＋b²＝0有实根的充要条件为Δ＝4a²－4b²≥0，即a≥b.

以下第一个数表示a的取值，第二个数表示b的取值．

总的基本事件共有12个：(1,2)，(1,3)，(1,4)，(2,1)，(2,3)，(2,4)，(3,1)，(3,2)，(3,4)，(4,1)，(4,2)，(4,3)．

事件A中包含6个基本事件：(2,1)，(3,1)，(3,2)，(4,1)，(4,2)，(4,3)．

事件A发生的概率为P(A)＝＝.

(2)先从袋中随机取一个球，放回后再从袋中随机抽取一个球，点P(m，n)的所有可能情况为：(1,1)，(1,2)，(1,3)，(1,4)，(2,1)，(2,2)，(2,3)，(2,4)，(3,1)，(3,2)，(3,3)，(3,4)，(4,1)，(4,2)，(4,3)，(4,4)，共16个．

点P(m，n)落在区域内的有(1,1)，(2,1)，(2,2)，(3,1)，共4个，

所以点P落在区域内的概率为.

18．(本小题满分12分)一般来说，一个人脚掌越长，他的身高就越高．现对10名成年人的脚掌长x与身高y进行测量．得到的数据(单位均为cm)作为一个样本如表所示.

(1)在上表数据中，以“脚掌长”为横坐标，“身高”为纵坐标，作出散点图后，发现散点在一条直线附近，试求“身高”与“脚掌长”之间的线性回归方程 ＝x＋ ；

(2)若某人的脚掌长为26.5 cm，试估计此人的身高；

(3)在样本中，从身高180 cm以上的4人中随机抽取2人作进一步的分析，求所抽取的2人中至少有1人身高在190 cm以上的概率．

(参考公式及数据：线性回归方程 ＝x＋ 中，＝， ＝－ ，其中，为样本平均值，(x_i－x)(y_i－y)＝577.5，(x_i－)²＝82.5)

解：(1)记样本中10人的“脚掌长”为x_i(i＝1,2，…，10)，

“身高”为y_i(i＝1,2，…，10)，

则 ＝＝＝7.

∵＝＝24.5，

＝＝171.5，

∴ ＝－ ＝0，

∴ ＝7x.

(2)由(1)知 ＝7x，当x＝26.5时，

　＝7×26.5＝185.5(cm)，

故估计此人的身高为185.5 cm.

(3)将身高为181 cm,188 cm,197 cm,203 cm的4人分别记为A，B，C，D.

记“从身高180 cm以上的4人中随机抽取2人作进一步的分析，所抽取的2人中至少有1人身高在190 cm以上” 为事件M，

则基本事件有(AB)，(AC)，(AD)，(BC)，(BD)，(CD)，共6个，

M包含的基本事件有(AC)，(AD)，(BC)，(BD)，(CD)，共5个，∴P(M)＝.

三、解答题

17．(本小题满分10分)[2014·湛江一测]甲、乙、丙三名优秀的大学毕业生参加一所重点中学的招聘面试，面试合格者可以签约．甲表示只要面试合格就签约，乙与丙则约定，两个面试都合格就一同签约，否则两人都不签约．设每人面试合格的概率都是P，且面试是否合格互不影响．已知至少有1人面试合格的概率为.

(1)求P；

(2)求签约人数ξ的分布列和数学期望．

解：(1)至少1人面试合格的概率为(包括1人合格、2人合格和3人都合格)，这样都不合格的概率为1－＝.

故(1－P)³＝，解得P＝.

(2)签约人数ξ的所有可能取值为0、1、2、3.

签约人数为0(甲不合格，乙、丙至少一人不合格)的概率为

P(ξ＝0)＝×(1－×)＝，

签约人数为1(甲合格，乙、丙至少一人不合格)的概率为

P(ξ＝1)＝×(1－×)＝，

签约人数为2(甲不合格，乙、丙全部合格)的概率为P(ξ＝2)＝×(1－)×(1－)＝，

签约人数为3(甲、乙、丙均合格)的概率为P(ξ＝3)＝()³＝.所以ξ的分布列为

数学期望E(ξ)＝0×＋1×＋2×＋3×＝1.

16．如图，⊙C内切于扇形AOB，∠AOB＝.若在扇形内任取一点，则该点在⊙C内的概率为________．

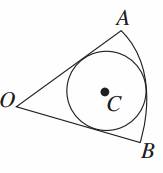
解析：设⊙C的半径为1，试验发生包含的事件对应的是扇形AOB，满足条件的事件是圆，⊙C的面积等于π.连接OC并延长交扇形于N.过C作CM⊥OB，则∠COM＝，OC＝2，ON＝3，∴扇形AOB的面积为××3²＝，∴⊙C的面积与扇形AOB的面积比是，∴所求概率P＝.

答案：

15．如图，运行程序框图后输出S的值是________．

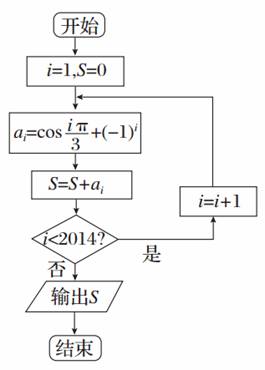
解析：因为a₁＋a₂＋a₃＋a₄＋a₅＋a₆＝0，且a_i＝a_i＋6，所以输出的S＝a₁＋a₂＋…＋a₂₀₁₄＝a₁＋a₂＋a₃＋a₄＝cos＋(－1)¹＋cos＋(－1)²＋cos＋(－1)³＋cos＋(－1)⁴＝－.

答案：－