
1.等腰三角形底边上的高与底边的比是1∶2,则它的顶角等于
A.90° B.60° C.120° D.150°
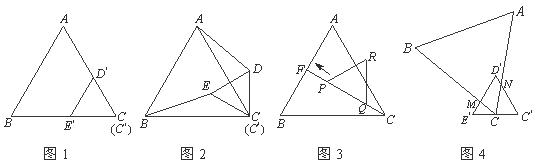
25.图1是边长分别为4和3的两个等边三角形纸片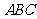 和
和 叠放在一起(
叠放在一起(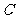 与
与 重合).
重合).
(1)固定△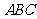 ,将△
,将△ 绕点
绕点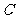 顺时针旋转
顺时针旋转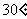 得到△
得到△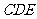 ,连结
,连结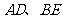 (如图2).此时线段
(如图2).此时线段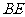 与
与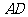 有怎样的数量关系?并证明你的结论;
有怎样的数量关系?并证明你的结论;
(2)设图2中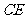 的延长线交
的延长线交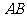 于
于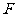 ,并将图2中的△
,并将图2中的△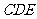 在线段
在线段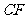 上沿着
上沿着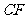 方向以每秒1个单位的速度平移,平移后的△
方向以每秒1个单位的速度平移,平移后的△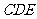 设为△
设为△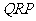 (如图3).设△
(如图3).设△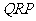 移动(点
移动(点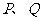 在线段
在线段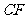 上)的时间为x秒,若△
上)的时间为x秒,若△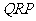 与△
与△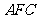 重叠部分的面积为y,求y与x之间的函数解析式,并写出自变量x的取值范围;
重叠部分的面积为y,求y与x之间的函数解析式,并写出自变量x的取值范围;
(3)若固定图1中的△ ,将△
,将△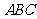 沿
沿 方向平移,使顶点C落在
方向平移,使顶点C落在 的中点处,再以点
的中点处,再以点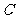 为中心顺时针旋转一定角度,设
为中心顺时针旋转一定角度,设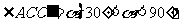 ,边
,边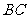 交
交 于点M,边
于点M,边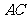 交
交 于点N(如图4).此时线段
于点N(如图4).此时线段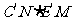 的值是否随
的值是否随 的变化而变化?如果没有变化,请你求出
的变化而变化?如果没有变化,请你求出 的值;如果有变化,请你说明理由.
的值;如果有变化,请你说明理由.
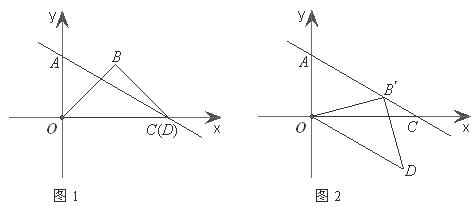
24.如图1,在平面直角坐标系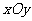 中,已知直线
中,已知直线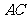 的解析式为
的解析式为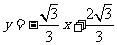 ,直线
,直线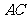 交
交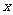 轴于点
轴于点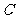 ,交
,交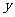 轴于点
轴于点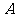 .
.
(1)若一个等腰直角三角板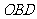 的顶点
的顶点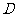 与点
与点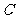 重合,求直角顶点
重合,求直角顶点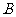 的坐标;
的坐标;
(2)若(1)中的等腰直角三角板绕着点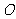 顺时针旋转,旋转角度为
顺时针旋转,旋转角度为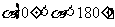 ,当点
,当点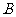 落在直线
落在直线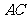 上的点
上的点 处时,求
处时,求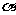 的值;
的值;
(3)在(2)的条件下,判断点 是否在过点
是否在过点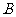 的抛物线
的抛物线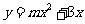 上,并说明理由.
上,并说明理由.
22.在平行四边形网格中,若它的每一个小平行四边形其中一边和这边上的高均为1个单位长,这样的平行四边形我们称为单位平行四边形.如图所示的每一个小平行四边形中,水平方向的边长均为1个单位.
(1)直接写出单位平行四边形的面积及图1中的四边形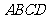 (顶点都在小平行四边形的顶点上)的面积;
(顶点都在小平行四边形的顶点上)的面积;
(2)请你在图2中画出两个面积都是12的图形,并使它们关于点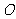 对称.
对称.
21.列方程(组)或不等式(组)解应用题:
净朋家政公司要临时招聘室内、室外两种家政员工共150人,室内、室外两种员工每月的保底工资分别为600元和1000元.因工作需要,要求室外员工的人数不可低于室内员工人数的2倍,那么招聘室内员工多少人时,可使此家政公司每月付的保底工资最少?最少为多少元?
20.今年昌平区初三学生的体育加试在5月完成,加试项目共三项,分别为:随机抽测项目(篮球)、必考项目(耐久跑:男生1000米,女生800米)和限制选项(男生实心球或引体向上,女生仰卧起坐或实心球),各项满分10分。夏明同学随机调查并统计本校的若干名初三学生有关体育加试的情况:
被调查学生参加考试情况统计表
|
参加考试情况 |
按时参加考试 |
参加缓考 |
免体 |
|
人数(单位:人) |
|
18 |
2 |
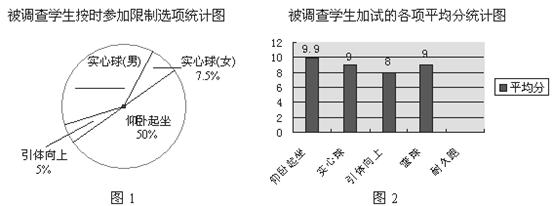
请你根据以上信息解答下列问题:
(1)在图1中,选择仰卧起坐的女生共40人,请补全图1和统计表;
(2)图1中表示参加实心球(女)的扇形的圆心角的度数;
(3)在图2中,若耐久跑的平均分是其他各项平均分的中位数,请补全图2;
(4)通过以上数据,你发现了什么,谈谈自己的看法或建议.
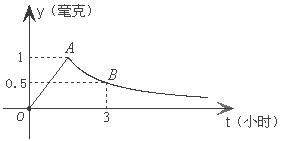
19.为了预防甲型H1N1流感,某校在周六那天用“药熏消毒法”对教室进行消毒.已知药物释放过程中,室内每立方米空气中的含药量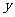 (毫克)与时间
(毫克)与时间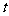 (小时)成正比;药物释放完毕后,
(小时)成正比;药物释放完毕后,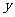 与
与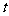 的函数关系式为
的函数关系式为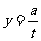 (
(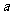 为常数),如图所示.根据图中提供的信息,解答下列问题:
为常数),如图所示.根据图中提供的信息,解答下列问题:
(1)写出从药物释放开始,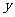 与
与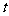 之间的两个函数关系式;
之间的两个函数关系式;
(2)据测定,当空气中每立方米的含药量降低到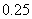 毫克以下时,对人无危害,那么从这次药物释放开始什么时间段内,学生在教室有危害?
毫克以下时,对人无危害,那么从这次药物释放开始什么时间段内,学生在教室有危害?
18.如图,点 在半⊙
在半⊙ 的直径
的直径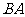 的延长线上,
的延长线上,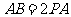 ,
,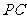 切半⊙
切半⊙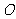 于点
于点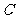 ,连结
,连结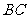 .
.
(1)求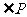 的正弦值;
的正弦值;
(2)若半⊙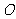 的半径为
的半径为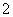 ,求
,求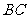 的长度.
的长度.
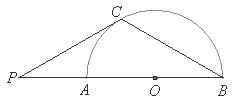
17.已知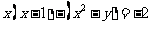 .求
.求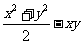 的值.
的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com