
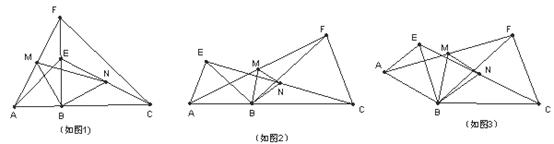
23.点A、B、C在同一直线上,在直线AC的同侧作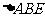 和
和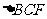 ,连接AF,CE.取AF、CE的中点M、N,连接BM,BN, MN.
,连接AF,CE.取AF、CE的中点M、N,连接BM,BN, MN.
(1)若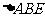 和
和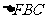 是等腰直角三角形,且
是等腰直角三角形,且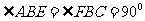 (如图1),则
(如图1),则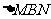 是 三角形.
是 三角形.
(2)在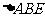 和
和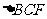 中,若BA=BE,BC=BF,且
中,若BA=BE,BC=BF,且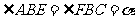 ,(如图2),则
,(如图2),则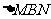 是
三角形,且
是
三角形,且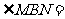 .
.
(3)若将(2)中的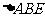 绕点B旋转一定角度,(如同3),其他条件不变,那么(2)中的结论是否成立? 若成立,给出你的证明;若不成立,写出正确的结论并给出证明.
绕点B旋转一定角度,(如同3),其他条件不变,那么(2)中的结论是否成立? 若成立,给出你的证明;若不成立,写出正确的结论并给出证明.
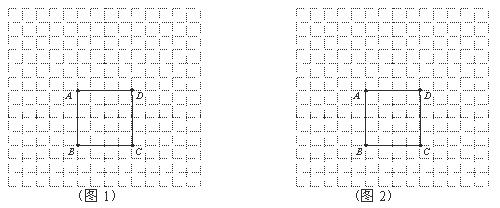
22.请设计一种方案:把正方形ABCD剪两刀,使剪得的三块图形能够拼成一个三角形,画出必要的示意图.
(1)使拼成的三角形是等腰三角形.(图1)
(2)使拼成的三角形既不是直角三角形也不是等腰三角形.(图2)
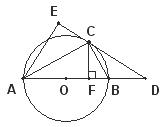
21. 如图,已知⊙O是△ABC的外接圆,AB是⊙O的直径,D是AB延长线的一点,AE⊥CD交DC的延长线于E,CF⊥AB于F,且CE=CF.
(1)求证:DE是⊙O的切线;
(2)若AB=6,BD=3,求AE和BC的长.
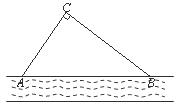
20. 某校把一块沿河的三角形废地(如图)开辟为生物园,已知∠ACB=90°,∠CAB=60°,AB=24米.为便于浇灌,学校在点C处建了一个蓄水池,利用管道从河中取水.已知每铺设1米管道费用为50元,求铺设管道的最低费用(精确到1元).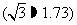
19.在一个不透明的口袋里,装着只有颜色不同的白、红、黑三种颜色的小球各一个.甲先从袋中随机摸出一球,看清颜色后放回,乙再从袋中随机摸出一球.
(1)画树状图(或列表),表示甲、乙摸球的所有可能结果.
(2)求乙摸到与甲相同颜色球的概率.
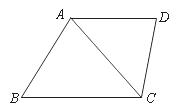
18.如图,在梯形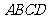 中,
中,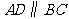 ,
, 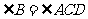 .
.
(1)请再写出图中另外一对相等的角;
(2)若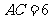 ,
,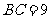 ,试求梯形AD的长.
,试求梯形AD的长.
17.已知关于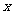 的一元二次方程
的一元二次方程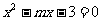 ,
,
(1)若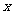 = -1是这个方程的一个根,求m的值
= -1是这个方程的一个根,求m的值
(2)对于任意的实数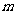 ,判断方程的根的情况,并说明理由.
,判断方程的根的情况,并说明理由.
16.化简: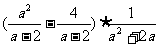 .
.
15.解方程: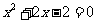 .
.
14.已知 ,求代数式
,求代数式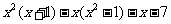 的值.
的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com