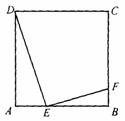
24．如图所示，E是正方形ABCD的边AB上的动点，EF⊥DE交BC于点F．

　 (1)求证：△ADE∽△BEF；

　 (2)设正方形的边长为4，AE=x，BF=y。当x取什么值时，y有最大值？并求出这个最大值；

　 (3)在(2)的条件下，当1＜x＜2时，求y的取值范围．

23．请你画一个以BC为底边的等腰三角形ABC，且使底边上的高AD=BC．

(1)求tanB与sinB的值；

(2)在你所画的等腰三角形ABC中，假设底边BC=5米，求腰上的高BE的长．

22．小明和小颖玩纸牌游戏．下面是同一副扑克中的4张扑克牌的正面，将它们正面朝下洗匀后放在桌子上，小明先从中抽出一张，小颖从剩余的3张牌中也抽出一张。小颖说：若抽出的两张牌的数字都是偶数，你获胜；否则，我获胜．

(1)请用树形图表示出两人抽牌可能出现的所有结果；

(2)若按小颖说的规则进行游戏，这个游戏公平吗？请说明理由．

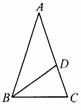
21．如图，在△ABC中，∠A=36°，AB=AC，BD是∠ABC的平分线，设CD=a，BD=b，AB=c．

　 (1)猜想a，b，c之间的数量关系，并说明理由；

　 (2)请你根据问题(1)提出一个问题，并说明理由．

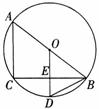
20．如图，AB是⊙O的直径，CB是弦，OD⊥CB于E，交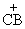于D，连接AC．

　 (1)请你写出三个不同类型的正确结论；

　 (2)若CB=8，ED=2，求⊙O的半径．

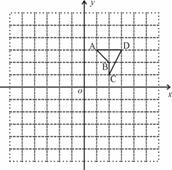
19．如图，在平面直角坐标系中，四边形ABCD的四个顶点的坐标分别是A(1，3)、

B(2，2)、C(2，1)，D(3，3)．

(1)以原点O为位似中心，相似比为2，将图形放大，画出符合要求的位似四边形；

(2)在(1)的前提下，写出点A的对应点坐标A′，并说明点A与点A′坐标的关系．

18．已知关于x的一元二次方程x²+kx－1=0．

(1)求证：方程有两个不相等的实数根；

(2)设方程的两根分别为x₁，x₂，且满足x₁+x₂=x₁·x₂，求k的值．

17．计算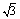sin60°－4cos²45°+sin30°tan45°．

16．如图，直角梯形ABCD中，∠BCD=90°，AD∥BC，BC=CD，E为梯形内一点，且∠BEC=90°，将△BEC绕C点旋转90°使BC 与DC重合，得到△DCF，连EF交CD于M，若BC=5，CF=3，则在下列四个结论中：①CE∥DF；②△DMF是等腰三角形；③EF平分∠CFD；④DM︰MC=4︰3．正确结论的序号是　 　　　　．

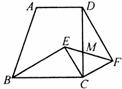
15．如图，⊙A、⊙B、⊙C相互外离，且它们的半径都是2，顺次连接三个圆的圆心得到三角形ABC，则图中三个扇形(阴影部分)的面积之和是　　　 ．