
(Ⅱ)设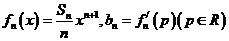 ,求数列
,求数列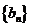 的前
的前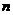 项和
项和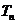 .
.
点评:考查归纳推理求通项公式,分类讨论的思想和方法.
㈣递推数列
(2007年全国卷II)设数列{an}的前n项和为Sn,且方程x2-anx-an=0有一根为Sn-1,n=1,2,3,….
(Ⅰ)求a1,a2;(Ⅱ){an}的通项公式.
点评:本题考查数列中通项an与前n项和Sn的关系,以及考查学生归纳、猜想、证明的思想.
(Ⅰ)写出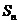 与
与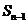 的递推关系式
的递推关系式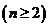 ,并求
,并求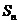 关于
关于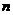 的表达式;
的表达式;
(2007年安徽卷)数列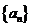 的前
的前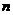 项和为
项和为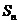 ,已知
,已知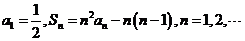
(注:无穷等比数列各项的和即当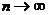 时该无穷数列前n项和的极限)
时该无穷数列前n项和的极限)
(Ⅲ)设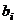 为数列
为数列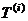 的第
的第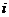 项,
项, ,求
,求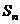 ,并求正整数
,并求正整数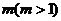 ,使得
,使得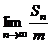 存在且不等于零.
存在且不等于零.
(Ⅱ)对给定的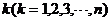 ,设
,设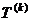 是首项为
是首项为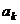 ,公差为
,公差为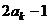 的等差数列.求数列
的等差数列.求数列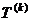 的前10项之和;
的前10项之和;
(Ⅰ)求数列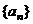 的首项
的首项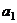 和公比
和公比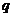 ;
;
(2007年广东卷)已知公比为 的无穷等比数列
的无穷等比数列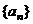 各项的和为9,无穷等比数列
各项的和为9,无穷等比数列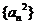 各项的和为
各项的和为 .
.
(3)记bn=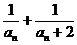 ,求数列{bn}的前n项和Sn,并证明Sn+
,求数列{bn}的前n项和Sn,并证明Sn+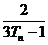 =1.
=1.
点评:本题主要考查数列中的基本知识,考查综合运用数学知识分析问题和解决问题的能力.解题时注意等比数列的概念及特殊数列的求和.
㈢数列求和
证明: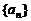 为等差数列的充分必要条件是
为等差数列的充分必要条件是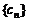 为等差数列且
为等差数列且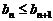 (n=1,2,3,…).
(n=1,2,3,…).
点评:本题主要考查等差数列、充要条件等基础知识,考查综合运用数学知识分析问题和解决问题的能力
㈡等比数列
(2007年山东卷)已知a1=2,点(an,an+1)在函数f(x)=x2+2x的图象上,其中n=1,2,3,…
(1)证明数列{lg(1+an)}是等比数列;
(2)设Tn=(1+a1) (1+a2) …(1+an),求Tn及数列{an}的通项;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com