
(Ⅲ)试求满足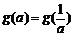 的所有实数a.
的所有实数a.
点评:本题主要考查函数、方程等基本知识,考查分类讨论的数学思想方法和综合运用数学知识分析问题和解决问题的能力.
㈡函数图像
(Ⅰ)设t=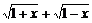 ,求t的取值范围,并把f(x)表示为t的函数m(t).
,求t的取值范围,并把f(x)表示为t的函数m(t).
(Ⅱ)求g(a);
(2007年江苏卷)设a为实数,记函数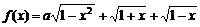 的最大值为g(a)。
的最大值为g(a)。
1.函数与导数
㈠函数与方程
(5)
证明不等式时,放缩法证明出现下列错误, 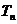 =
=

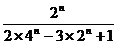 =
=

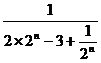 <
<

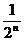 ,从而得出
,从而得出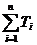 <
< (
(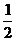 +
+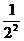 +…+
+…+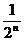 )=
)= (1-
(1-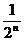 )<
)< ,其中2
,其中2
 -3+
-3+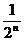 >
> 在n=1时不成立.
在n=1时不成立.
(6) 计算出错也是本题失分的重要原因.
[复习提示]:
对递推数列及数列与不等式相结合的题型的考查近几年越来越成为高考的热点和难点,在复习时应注意以下几个问题:
(1) 通过递推数列研究数列的性质及求通项的方法;
(2) 数列求和常用方法(如本题用到的裂项相消法)的分析;
(3) 建立在数列背景下的不等式的证明方法(如分析法、数学归纳法、放缩法及利用数列的单调性求解等).
我们把高考数学内容基础知识分成七部分,函数与导数,数列,不等式,平面向量和三角函数(含三角形),立体几何,解析几何),和概率统计(含排列组合、二项式定理). 有的题目考查了多项知识,也是归在一类里.下面结合2007年各地高考试题分专题介绍考查的基本内容和方法。
(4)
写出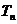 =
=

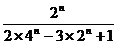 ,没有分解因式及拆项的意识,从而解答不够彻底.
,没有分解因式及拆项的意识,从而解答不够彻底.
(3)
第(Ⅱ)问把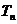 错误地认为是
错误地认为是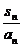 而出错.
而出错.
(2)
在写递推关系 =4
=4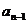 +
+ 后,得出
后,得出 +
+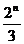 =4(
=4(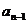 +
+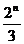 ),从而认为数列{
),从而认为数列{ +
+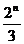 }为等比数列而出错.
}为等比数列而出错.
(1)
把 =
=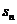 -
-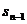 错写为
错写为 =
=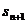 -
-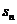 而出错.
而出错.
所以,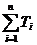 =
= 
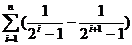 =
=
 (
(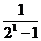 -
-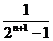 ) <
) < .
.
从以上分析可以看出,解决本题的难点有两个,一是对递推关系的变形,二是求和时裂项的技巧.对这两个难点的突破,是解决本题的关键.
[错因分析]:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com