3．（2007年湖北卷）在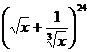的展开式中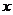，的幂的指数是整数的项共有  （C）

A.3项               B.4项             C.5项              D.6项

2．（2007年陕西卷）展开式中的常数项为＿594＿（用数字作答）。

1．（2007年福建卷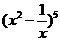）展开式中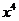的系数是＿10＿（用数字作答）。

7．(2007年山东卷）已知集合A=｛5｝,B=｛1,2｝,C=｛1,3,4｝，从这三个集合中各取一个元素构成空间直角坐标系中点的坐标，则确定的不同点的个数为 (A)

(A)33         (B) 34           (C) 35               (D)36

㈡二项式定理

6．（ 2007年浙江卷）函数f: {1,2,3}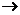{1,2,3}满足f(f(x))= f(x)，则这样的函数个数共有 ( D )

(A)1个            (B)4个           (C)8个             (D)10个

5．（2007年上海卷）如果一条直线与一个平面垂直，那么，称此直线与平面构成一个“正交线面对”．在一个正方体中，由两个顶点确定的直线与含有四个顶点的平面构成的“正交线面对”的个数是    36      ．

4．（2007年辽宁卷）5名乒乓球队员中,有2名老队员和3名新队员.现从中选出3名队员排成1、2、3号参加团体比赛,则入选的3名队员中至少有一名老队员,且1、2号中至少有1名新队员的排法有_______种.(以数作答)

【点评】本题考查了有限制条件的排列组合问题以及分类讨论思想.

3．（2007年江苏卷）今有2个红球、3个黄球、4个白球，同色球不加以区分，将这9个球排成一列有　▲　种不同的方法（用数字作答）。

点评：本题主要考查不全相异元素的全排列

2．（2007年湖北卷）某工程队有6项工程需要先后单独完成，其中工程乙必须在工程甲完成后才能进行，工程丙必须在工程乙完成后进行，又工程丁必须在丙完成后立即进行，那么安排这6项工程的不同的排法种数是__20________.（用数字作答）

1．( 2007年重庆卷)将5名实习教师分配到高一年级的３个班实习，每班至少１名，最多２名，则不同的分配方案有  ( B )

（A）３０种　　　（B）９０种    （C）１８０种　　　（D）２７０种