
若1< a <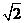 , 则当y = -1时, | PQ | 取最大值2 .
, 则当y = -1时, | PQ | 取最大值2 .
解法2:
若a ≥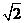 , 则
, 则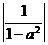 ≤1, 当y =
≤1, 当y = 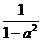 时, | PQ | 取最大值
时, | PQ | 取最大值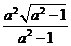 ;
;
= (1 )
) 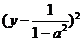
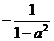 + 1 +
+ 1 + 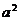 .
.
因为 | y | ≤ 1, a > 1,
= (1 )
)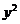 -2y + 1 +
-2y + 1 + 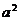
 =
= 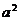 (1
(1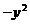 ) +
) + 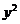 -2y + 1
-2y + 1
又因为Q在椭圆上, 所以 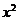 =
= 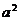 (1
(1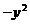 ) .
) .
解法1: 依题意可设 P (0, 1 ), Q (x
, y ), 则| PQ | = 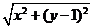 .
.
[解答分析] 要求| PQ |的最大值, 为方便, 对 加以讨论. 首先需写出点P、Q的坐标. 因Q在椭圆上, 通过消元法消去
加以讨论. 首先需写出点P、Q的坐标. 因Q在椭圆上, 通过消元法消去 中的一个未知数(这里消x), 得到
中的一个未知数(这里消x), 得到 关于y的表达式, 是一个y的二次式, 配平方. 其中有参数a, 需结合此椭圆的性质分类讨论, 从而求出| PQ |的最大值.
关于y的表达式, 是一个y的二次式, 配平方. 其中有参数a, 需结合此椭圆的性质分类讨论, 从而求出| PQ |的最大值.
本题属于难题, 区分度较好. 六道解答题中, 本题不能入门得0分者最多, 达57%. 除此之外, 得分主要分布在1~6分. 仅写出P、Q的坐标得1~2分者有约五分之一, 能写出| PQ |的表达式并消元得5~6分者有7%, 进一步将 的表达式配平方, 而未加讨论写出| PQ |的最大值得8~9分者有7%, 基本完成解答, 得10分及其以上者有3%, 得满分者为1.3%.
的表达式配平方, 而未加讨论写出| PQ |的最大值得8~9分者有7%, 基本完成解答, 得10分及其以上者有3%, 得满分者为1.3%.
[考查意图] 本题主要考查椭圆的基本知识、两点间的距离及综合分析问题的能力.
0.13
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com