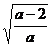(-∞, -)

(?) 当a>2时, 解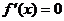得x =±,

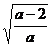x

(?) 当a=2时, 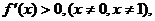故f (x) 在区间 (-∞, 1), (1, +∞)仍为增函数.

       .

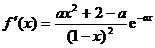(?) 当0<a<2时, 导数恒正, 故f (x) 在区间 (-∞, 1), (1, +∞) 为增函数.

    本小题是一道难题, 也是全卷最难的一道题; 区分度较好. 分数分布呈现出分数越高人数越少的状态: 得零分的考生约占32％, 会求导数而得到1~3分者约占37％, 再会利用导数判断函数的单调性而得4~6分者约占18％, 能对参数进行讨论而得7~10分者约占11.5％; 得11~13分者约占1.5%, 得满分者仅占0.07％.

[考查意图] 本小题主要考查分类讨论的数学思想和导数的计算、应用导数研究函数单调性的基本方法，考查逻辑推理能力.

[解答分析] 本小题的解法是常规方法, 但需要我们函数概念清楚、逻辑推理能力强. 解答时需要注意三点, 一是本类题目应该对参数a进行分类讨论, 而不是对函数的定义域分类讨论, 具体到本小题, 应该分0<a<2, a=2, a>2三种情况讨论. 二是在函数单调性判定定理“在一个区间上导数恒正（负）, 则函数在这个区间上单增（减）”中,“区间”这个条件也是不能少的, 本小题函数的定义域不是区间, 需要把定义域分成区间, 再判定函数在每一区间的单调性. 三是注意细节, 如数学符号书写应该正确, 以及本小题两问中参数a的变化范围不同. 参考解答如下.

解 (Ⅰ) 函数f (x)的定义域为(-∞, 1)∪(1, +∞), 导数为

   0.19

   2.59

已知函数 .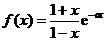

(Ⅰ) 设a >0, 讨论 y = f (x) 的单调性;

(Ⅱ) 若对任意 x∈(0,1) 恒有 f (x) >1, 求 a的取值范围.

[抽样统计数据]

题号

满分

  平均分

   难度

  理(21)

    14

    此外, 有的考生是用解法2求解, 在设Q (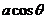, 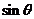)时, 不恰当的限定θ的范围, 如: θ∈[0,π] 或θ∈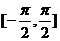. 这样做改变了点Q 的属性, 因为, 当θ∈[0,π]时, Q 只在上半椭圆, 当θ∈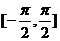时, 点Q 只在右半椭圆.

    [复习提示] 注意“读题”, 即分析题目, 挖掘其中的信息. 解题中注意每一处细节, 培养思维的严谨周密. 消元时需注意被消变量的选择, 要使消元的过程尽可能简单, 消元后的结果尽可能方便使用.

理（21）（本小题满分14分）

    有的考生虽知道要对a分类讨论, 但未找到恰当的分类标准, 导致失误. 分类应从所研究的具体问题出发, 去选择恰当的分类标准, 不重不漏地将讨论对象划分为若干个类别. 具体到此问题, 则应是注意到 | y | ≤ 1, a > 1, 从是否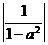≤1来考虑分类.