
(2)把 =
=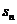 -
-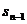 代入原递推关系转化为
代入原递推关系转化为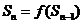 型的递推关系,即把
型的递推关系,即把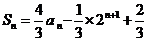 ,
,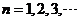 ,化为
,化为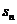 =4
=4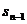 +
+ -2, n=2,3…;(3)利用迭代的思想解决问题;(4)根据递推关系写出数列的前几项,猜出数列的通项公式,然后利用数学归纳法证明.
-2, n=2,3…;(3)利用迭代的思想解决问题;(4)根据递推关系写出数列的前几项,猜出数列的通项公式,然后利用数学归纳法证明.
[解答分析](Ⅰ)本题所涉及的递推数列是 型,这种类型的递推数列求首项
型,这种类型的递推数列求首项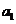 可通过解关于
可通过解关于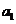 的方程
的方程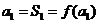 求出,而求数列
求出,而求数列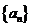 的通项公式可考虑以下三种手段:(1)利用
的通项公式可考虑以下三种手段:(1)利用 =
=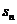 -
-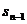 把原递推关系转化为
把原递推关系转化为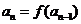 型的递推关系,即把
型的递推关系,即把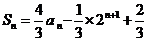 ,
,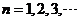 化为
化为 =4
=4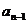 +
+ ;
;
这是一道难题, 区分度较好. 本题得零分者有约10.5%, 作为压轴题并不算高, 可见入手并不难. 得分在1-2分者占16.6 %,得分在3-4分者占59.7 %,这些是多多少少会用些数列的性质, 得分在5-6分者占5.1 %,这些是看出数列通项的规律,或求出通项的,做到第(Ⅱ)问得分在7-11分者占7.82 %,得满分者占千分之三.
[考查意图]:本题主要考查数列和等比数列的基本知识,递推数列求通项公式,数列求和及不等式证明等思想和方法.
0.29
3.42
(Ⅱ)设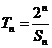 ,
,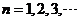 ,证明:
,证明: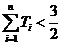 .
.
[抽样统计数据]
题号
满分
平均分
难度
理(22)
12
(Ⅰ)求首项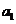 与通项
与通项 ;
;
理(22) 设数列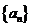 的前
的前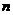 项的和
项的和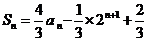 ,
,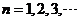
得到结果: 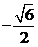 ≤ a ≤-1 或 1≤ a ≤
≤ a ≤-1 或 1≤ a ≤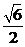 . 错在未能从
. 错在未能从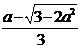 ≥0中推出a > 0和未顾及到Δ> 0时有-
≥0中推出a > 0和未顾及到Δ> 0时有-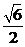 < a <
< a < 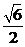 . 还有的考生在解
. 还有的考生在解 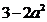 = 0时得到错解:x=
= 0时得到错解:x=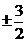 或
或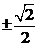 或
或 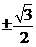 ; 将
; 将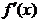 的图象的对称轴错为 x =
的图象的对称轴错为 x =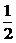 等.
等.
[复习提示] 应准确理解掌握导数与函数性质的关系. 纯代数的方法有时会较繁琐, 甚至不能解决问题, 应注意掌握数形结合的思想方法. 分类讨论须紧贴题目, 根据解题需要确定恰当的分类标准, 使得分类不重不漏.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com