
3.(2007年天津卷)如图,以椭圆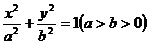 的中心
的中心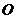 为圆心,分别以
为圆心,分别以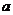 和
和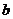 为半径作大圆和小圆.过椭圆右焦点
为半径作大圆和小圆.过椭圆右焦点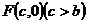 作垂直于
作垂直于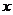 轴的直线交大圆于第一象限内的点
轴的直线交大圆于第一象限内的点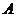 .连结
.连结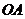 交小圆于点
交小圆于点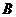 .设直线
.设直线 是小圆的切线.
是小圆的切线.
 点评:本小题主要考察双曲线的定义和性质、直线与双曲线的关系、点到直线的距离等知识及解析几何的基本思想、方法和综合解决问题的能力.满分12分.
点评:本小题主要考察双曲线的定义和性质、直线与双曲线的关系、点到直线的距离等知识及解析几何的基本思想、方法和综合解决问题的能力.满分12分.
2.(2007年四川卷)已知两定点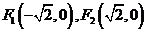 ,满足条件
,满足条件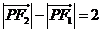 的点
的点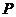 的轨迹是曲线
的轨迹是曲线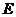 ,直线
,直线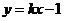 与曲线
与曲线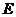 交于
交于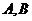 两点,如果
两点,如果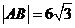 ,且曲线
,且曲线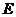 上存在点
上存在点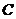 ,使
,使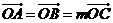 ,求
,求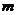 的值和
的值和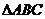 的面积
的面积 .
.
(2) 过点P(0,4)的直线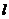 ,交双曲线C于A,B两点,交x轴于Q点(Q点与C的顶点不重合).当
,交双曲线C于A,B两点,交x轴于Q点(Q点与C的顶点不重合).当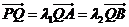 ,且
,且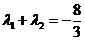 时,求Q点的坐标.
时,求Q点的坐标.
点评:本题主要考查椭圆与双曲线的基本概念、标准方程、几何性质等基础知识和基本运算能力.
1.(2007年山东卷)双曲线C与椭圆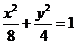 有相同的焦点,直线y=
有相同的焦点,直线y=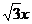 为C的一条渐近线.
为C的一条渐近线.
(1) 求双曲线C的方程;
(Ⅱ)是否存在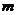 、
、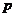 的值,使抛物线C2的焦点恰在直线AB上?若存在,求出符合条件的
的值,使抛物线C2的焦点恰在直线AB上?若存在,求出符合条件的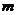 、
、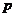 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
点评:本题主要考查直线与椭圆的位置关系,抛物线的定义等问题,考查学生计算、数形结合等方面综合的能力.
㈥解析几何与向量相结合:注意平面几何知识的应用
(Ⅰ)当AB⊥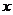 轴时,求
轴时,求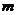 、
、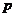 的值,并判断抛物线C2的焦点是否在直线AB上;
的值,并判断抛物线C2的焦点是否在直线AB上;
3.( 2007年湖南卷)已知椭圆C1: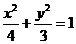 ,抛物线C2:
,抛物线C2: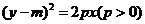 ,且C1、C2的公共弦AB过椭圆C1的右焦点.
,且C1、C2的公共弦AB过椭圆C1的右焦点.
(Ⅱ)若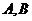 是
是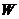 上的不同两点,
上的不同两点,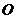 是坐标原点,求
是坐标原点,求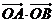 的最小值.
的最小值.
点评:考查双曲线的定义,以及利用代数的方法―坐标法解决几何问题,会转化为函数的最值,又考查分类讨论的思想和函数思想.
(Ⅰ)求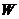 的方程;
的方程;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com