
 ㈥数列应用
㈥数列应用
点评:本题以新名词“绝对差数列”出现,考查学生构造新数列的能力;以及利用已知条件,通过观察、归纳、证明的能力. 其中(Ⅱ)可说明数列 是周期数列,而
是周期数列,而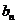 是常数列;(Ⅲ)要求学生有较深厚的数学功底,可考虑使用反证法与放缩法证明.
是常数列;(Ⅲ)要求学生有较深厚的数学功底,可考虑使用反证法与放缩法证明.
(Ⅱ)若“绝对差数列”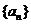 中,
中,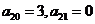 ,数列
,数列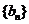 满足
满足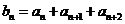 ,
,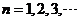 ,分别判断当
,分别判断当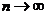 时,
时, 与
与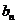 的极限是否存在,如果存在,求出其极限值;
的极限是否存在,如果存在,求出其极限值;
(Ⅲ)证明:任何“绝对差数列”中总含有无穷多个为零的项.
(2007年北京卷)在数列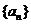 中,若
中,若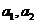 是正整数,且
是正整数,且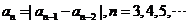 ,则称
,则称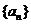 为“绝对差数列”.
为“绝对差数列”.
(Ⅰ)举出一个前五项不为零的“绝对差数列”(只要求写出前十项);
(3)若(2)中的数列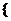
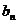
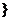 满足不等式|
满足不等式|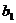 -
- |+|
|+|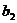 -
- |+┅+|
|+┅+|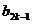 -
- |+|
|+|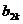 -
- |≤4,求
|≤4,求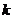 的值.
的值.
点评:本题主要考查等比数列的基本知识.
㈤新定义型数列
(2)若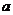 =2
=2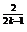 ,数列
,数列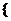
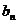
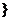 满足
满足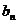 =
=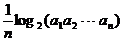 (
(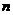 =1,2,┅,2
=1,2,┅,2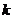 ),求数列
),求数列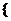
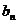
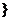 的通项公式;
的通项公式;
(1)求证:数列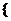

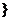 是等比数列;
是等比数列;
(2007年上海卷)已知有穷数列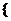

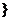 共有2
共有2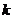 项(整数
项(整数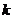 ≥2),首项
≥2),首项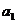 =2.设该数列的前
=2.设该数列的前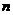 项和为
项和为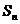 ,且
,且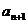 =
=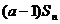 +2(
+2(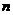 =1,2,┅,2
=1,2,┅,2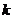 -1),其中常数
-1),其中常数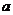 >1.
>1.
点评:此题主要考查怎样用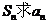 ,注意分两步进行.
,注意分两步进行.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com