 点评:在立体几何学习中,我们要多培养空间想象能力, 对于图形的翻折问题,关健是利用翻折前后的不变量,二面角的平面角的适当选取是立体几何的核心考点之一.是高考数学必考的知识点之一.作,证,解,是我们求二面角的三步骤.作:作出所要求的二面角,证:证明这是我们所求二面角,并将这个二面角进行平面化,置于一个三角形中,最好是直角三角形,利用我们解三角形的知识求二面角的平面角.向量的运用也为我们拓宽了解决立体几何问题的角度,不过在向量运用过程中,要首先要建系,建系要建得合理,最好依托题目的图形,坐标才会容易求得.
点评:在立体几何学习中,我们要多培养空间想象能力, 对于图形的翻折问题,关健是利用翻折前后的不变量,二面角的平面角的适当选取是立体几何的核心考点之一.是高考数学必考的知识点之一.作,证,解,是我们求二面角的三步骤.作:作出所要求的二面角,证:证明这是我们所求二面角,并将这个二面角进行平面化,置于一个三角形中,最好是直角三角形,利用我们解三角形的知识求二面角的平面角.向量的运用也为我们拓宽了解决立体几何问题的角度,不过在向量运用过程中,要首先要建系,建系要建得合理,最好依托题目的图形,坐标才会容易求得.
例2 (2007广东卷)如图所示,AF、DE分别是⊙O、⊙O1的直径.AD与两圆所在的平面均垂直,AD=8,BC是⊙O的直径,AB=AC=6,OE//AD.
(Ⅰ)求二面角B―AD―F的大小;(Ⅱ)求直线BD与EF所成的角.
分析:本题主要考查异面直线所成的角及二面角的一般求法,综合性较强,可利用传统方法和空间向量的方法解决.
(三)求空间距离
空间中距离的求法是历年高考考查的重点,其中以点与点、点到线、点到面的距离为基础,求其他几种距离一般化归为这三种距离.
空间中的距离主要指以下七种:(1)两点之间的距离;(2)点到直线的距离;(3)点到平面的距离;(4)两条平行线间的距离;(5)两条异面直线间的距离;(6)平面的平行直线与平面之间的距离;(7)两个平行平面之间的距离.

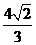 (D)
(D)