
3.设随机变量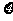 的分布列由
的分布列由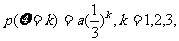 则
则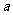 的值为
( )
的值为
( )
A.1
B.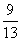 C.
C.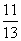 D.
D.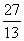
2.若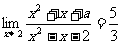 ,则
,则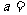 ( )
( )
A.2
B.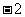 C.
C.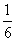 D.
D.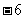
1.复数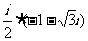 的虚部是 ( )
的虚部是 ( )
A.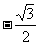 B.
B. 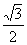 C.
C. 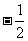 D.
D.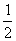
22.(本小题满分14分)
已知在平面直角坐标系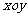 中,向量
中,向量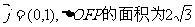 ,且
,且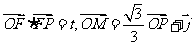 .
.
(1)设 的取值范围;
的取值范围;
(2)设以原点O为中心,对称轴在坐标轴上,以F为右焦点的椭圆经过点M,且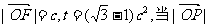 取最小值时,求椭圆的方程.
取最小值时,求椭圆的方程.
21.(本小题满分12分)
设数列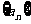 是等比数列,
是等比数列,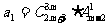 ,公比q是
,公比q是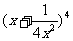 的展开式中的第二项(按x的降幂排列),
的展开式中的第二项(按x的降幂排列),
(1)用n,x表示通项an与前n项和Sn
(2)若An=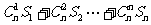 ,用n,x表示An
,用n,x表示An
20.(本小题满分12分)
已知正方体ABCD-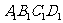 中,E为棱CC
中,E为棱CC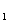 上的动点,
上的动点,
(1)求证: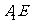 ⊥
⊥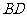 ;
;
(2)当E恰为棱CC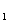 的中点时,求证:平面
的中点时,求证:平面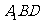 ⊥
⊥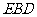 ;
;
(3)在棱CC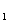 上是否存在一个点
上是否存在一个点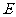 ,可以使二面角
,可以使二面角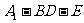 的大小为45°,如果存在,试确定点
的大小为45°,如果存在,试确定点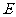 在棱CC
在棱CC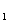 上的位置;如果不存在,请说明理由.
上的位置;如果不存在,请说明理由.
19.(本小题满分12分)
已知实数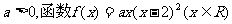 有极大值32.
有极大值32.
(1)求函数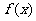 的单调区间;
的单调区间;
(2)求实数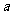 的值.
的值.
18.(本小题满分12分)
(文)甲、乙二人做射击游戏,甲、乙射击击中与否是相互独立事件.规则如下:若射击一次击中,则原射击人继续射击;若射击一次不中,就由对方接替射击.已知甲、乙二人射击一次击中的概率均为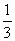 ,且第一次由甲开始射击.
,且第一次由甲开始射击.
(1)求前3次射击中甲恰好击中2次的概率;
(2)求第4次由甲射击的概率.
(理)已知某车站每天8:00-9:00、9:00-10:00都恰好有一辆客车到站;8:00-9:00到站的客车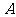 可能在8:10、8:30、8:50到,其概率依次为
可能在8:10、8:30、8:50到,其概率依次为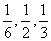 .9:00-10:00到站的客车
.9:00-10:00到站的客车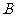 可能在9:10、9:30、9:50到,其概率依次为
可能在9:10、9:30、9:50到,其概率依次为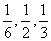 .今有甲、乙两位旅客,他们到站的时间分别为8:00和8:20,试问他们候车时间的平均值哪个更多?
.今有甲、乙两位旅客,他们到站的时间分别为8:00和8:20,试问他们候车时间的平均值哪个更多?
17.(本小题满分12分)
(文)已知: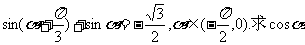 .
.
(理)已知函数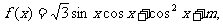 其中m为实常数
其中m为实常数
(1)求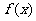 的最小正周期;
的最小正周期;
(2)设集合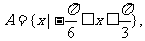 已知当
已知当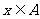 时,
时,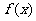 的最小值为2,当
的最小值为2,当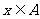 时,求
时,求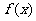 的最大值.
的最大值.
16.已知等式: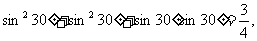
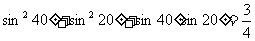
请你写出一个具有一般性的等式,使你写出的等式包含了已知的等式(不要求证明)这个等式是___________________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com