
6.甲袋中装有3个白球5个黑球,乙袋中装有4个白球6个黑球,现从甲袋中随机取出一个球放入乙袋中,充分惨混后再从乙袋中随机取出一个球放回甲袋,则甲袋中白球没有减少的概率为 ( )
A.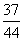 B.
B.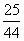 C.
C.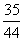 D.
D.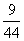
5.一个球的内接正四棱柱的侧面积与上下两底面积的和之比为4:1,且该正四棱柱的体积为
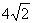 ,则这个球的表面积为 ( )
,则这个球的表面积为 ( )
A.12 B.12π C.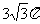 D.12
D.12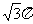
4.函数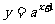 的图象与函数
的图象与函数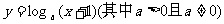 的图象关于 ( )
的图象关于 ( )
A.直线y= x对称 B.直线y=x-1对称
C.直线y= x +1对称 D.直线y=-x+1对称
3.已知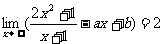 ,则b的值为 ( )
,则b的值为 ( )
A.0 B.4 C.-4 D.不确定
2.函数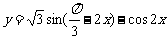 的最小值为 ( )
的最小值为 ( )
A.-1 B.-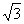 -1 C.-
-1 C.-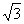 D.0
D.0
1.已知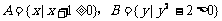 ,全集I=R,则A∩
,全集I=R,则A∩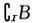 为 ( )
为 ( )
A.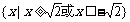 B.
B.
C.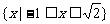 D.
D.
22.(本小题12分)
已知函数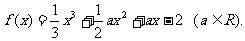
(1)若函数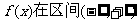 上为单调函数,求实数a的取值范围;
上为单调函数,求实数a的取值范围;
(2)设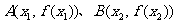 是函数
是函数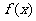 的两个极值点,若直线AB的斜率不小
的两个极值点,若直线AB的斜率不小
于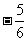 ,求实数a的取值范围.
,求实数a的取值范围.
21.(本小题12分)
已知双曲线的两条渐近线方程为直线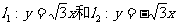 ,其焦点在x轴上,实轴长为2.
,其焦点在x轴上,实轴长为2.
(Ⅰ)求双曲线的方程;
(Ⅱ)设直线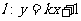 与双曲线相切于点M且与右准线交于N,F为右焦点,求证:∠MFN为直角.
与双曲线相切于点M且与右准线交于N,F为右焦点,求证:∠MFN为直角.
20.(本小题12分)
设数列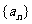 前n项和为Sn,且
前n项和为Sn,且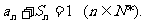
(Ⅰ)求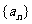 的通项公式;
的通项公式;
(Ⅱ)若数列{bn}满足b1=1且bn+1=bn+an(n≥1),求数列{bn}的通项公式
19.(本小题12分)
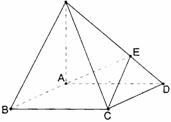
如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=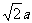 ,点E在PD上,且PE :
ED=2 : 1.
,点E在PD上,且PE :
ED=2 : 1.
(1)证明:PA⊥平面ABCD;
(2)求以AC为棱EAC与DAC为面的二面角θ的大小.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com