
20.某单位建造一间地面面积为12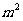 的背面靠墙的矩形小房,由于地理位置的限制,房子侧面的长度
的背面靠墙的矩形小房,由于地理位置的限制,房子侧面的长度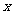 不得超过
不得超过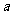 米,房屋正面的造价为400元/
米,房屋正面的造价为400元/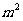 ,房屋侧面的造价为l50元/
,房屋侧面的造价为l50元/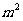 ,屋顶和地面的造价费用合计为5800元,如果墙高为3
,屋顶和地面的造价费用合计为5800元,如果墙高为3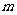 ,且不计房屋背面的费用。
,且不计房屋背面的费用。
(1)把房屋总造价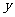 表示成
表示成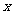 的函数,并写出该函数的定义域;
的函数,并写出该函数的定义域;
(2)当侧面的长度为多少时,总造价最底?最低总造价是多少?
19.(选一)已知等差数列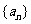 的公差大于
的公差大于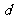 0,且
0,且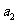 、
、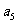 是方程
是方程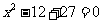 的两根,数列
的两根,数列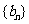 的前项
的前项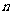 和为
和为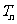 ,且
,且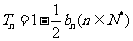 。
。
(1)求数列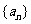 、
、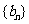 的通项公式;
的通项公式;
(2)记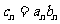 ,求数列
,求数列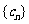 的前
的前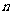 项和
项和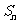 。
。
(选二)现有甲、乙两个盒子,甲盒子里盛有4个白球和4个红球,乙盒子里盛有3个白球和若干个红球若从乙盒子里任取两个球,取到同色球的概率是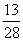 。
。
(1)求乙盒子里红球的个数;
(2)若从甲盒子里任意取出两个球,放入乙盒子里充分搅拌均匀后,再从乙盒子里任意取出2个球放回甲盒子里,求甲盒子里的白球没有变化的概率。
18.已知向量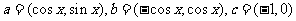 。
。
(1)若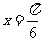 ,求向量
,求向量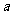 、
、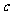 的夹角;
的夹角;
(2)当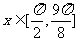 时,求函数
时,求函数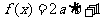 的最大值。
的最大值。
17.已知集合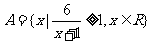 ,
, 。
。
(1)当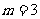 时,求
时,求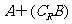 ;
;
(2)若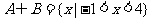 ,求实数
,求实数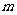 的值。
的值。
16.对于任意的两个实数对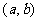 和
和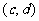 ,规定:
,规定:
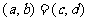 ,当且仅当
,当且仅当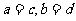 时成立
时成立
运算“ ”为:
”为: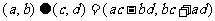 ,
,
运算“ ”为:
”为: 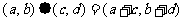 。
。
现设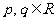 ,若
,若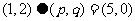 ,则
,则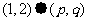 = 。
= 。
15.(选一)定义“等积数列”为:数列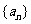 中,对任意
中,对任意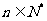 ,都有
,都有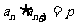 (常数),则数列
(常数),则数列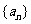 为等积数列,
为等积数列,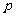 为公积。现已知数列
为公积。现已知数列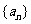 为等积数列,且
为等积数列,且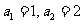 ,则当
,则当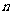 为奇数时,其前
为奇数时,其前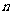 项和
项和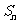 = 。
= 。
(选二)甲乙两支排球队进行一场比赛,比赛采用五局三胜制,即首先赢得三场比赛的队获胜且比赛结束,已知在每一局比赛中甲队战胜乙队的概率是0.6,且各局比赛之间没有影响,现在已知乙队已经赢了第一局,则最终甲队获胜的概率是 。
14.已知函数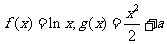 ,直线
,直线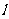 与
与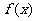 、
、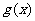 的图像均相切,且
的图像均相切,且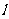 与的图像
与的图像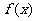 的切点的横坐标为1,则实数的
的切点的横坐标为1,则实数的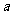 值为 。
值为 。
13.已知向量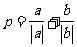 ,其中
,其中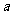 、
、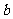 均为非零向量,则
均为非零向量,则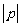 的取值范围是 。
的取值范围是 。
12.已知函数①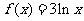 ;②
;②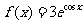 ;③
;③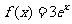 ;④
;④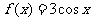 ,其中对于
,其中对于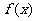 定义域内的任意一个自变量
定义域内的任意一个自变量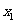 都存在唯一自变量
都存在唯一自变量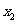 ,使
,使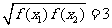 成立的函数是(
)
成立的函数是(
)
A.①②④ B.②③ C.③ D.④
第Ⅱ卷 (非选择题 共90分)
11.设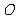 为坐标原点,点
为坐标原点,点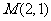 ,点
,点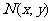 满足
满足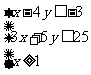 ,则的最大值为(
)
,则的最大值为(
)
A.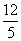 B.
B.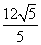 C.
C.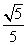 D.
D.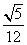
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com