
3.已知命题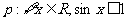 ,则 ( )
,则 ( )
A.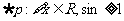 B.
B.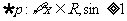
C.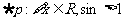 D.
D.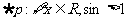
2.已知集合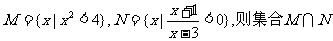 = ( )
= ( )
A.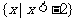 B.
B.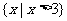
C.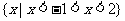 D.
D.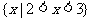
1.若复数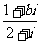 是纯虚数(i是虚数单位,b是实数),则b= ( )
是纯虚数(i是虚数单位,b是实数),则b= ( )
A.2 B.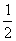 C.-
C.-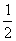 D.-2
D.-2
22.(本小题满分12分)
(文)已知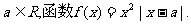
(I)当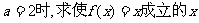 的集合;
的集合;
(II)当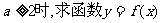 在区间[1,2]上的最小值。
在区间[1,2]上的最小值。
(理)已知函数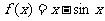
证明:(1)或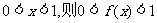 ;
;
(2)若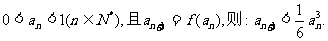
21.(本小题满分12分)
(文)直线l过抛物线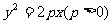 的焦点,且与抛物线相交于
的焦点,且与抛物线相交于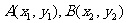 两点。
两点。
(I)求证: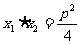 ;
;
(II)求证:对于抛物线的任意给定的一条弦CD,直线l不是CD的垂直平分线。
(理)已知数列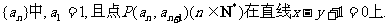
(I)若函数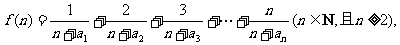 求证:
求证: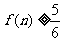 ;
;
(II)设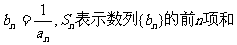 。试问:是否存在关于n的整式g(n),使得
。试问:是否存在关于n的整式g(n),使得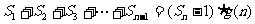 对于一切不小于2的自然数n恒成立?若不存在,试说明理由;若存在,写现g(n)的解析式,并加以证明。
对于一切不小于2的自然数n恒成立?若不存在,试说明理由;若存在,写现g(n)的解析式,并加以证明。
20.(本小题满分12分)
(文)(本小题满分12分)
已知正数数列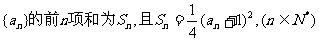
(I)求数列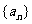 的通项公式(写出推导过程);
的通项公式(写出推导过程);
(II)设
(理)直线l过抛物线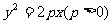 的焦点,且与抛物线相交于
的焦点,且与抛物线相交于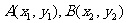 两点。
两点。
(I)求证: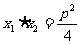 ;
;
(II)求证:对于抛物线的任意给定的一条弦CD,直线l不是CD的垂直平分线。
19.(本小题满分12分)
直三棱柱ABC-A1B1C1中,AC=CB=AA1=2,∠ACB=90°,E是BB1的中点,D为AB的中点。
(I)求证:DE⊥平面A1CD;
(II)求二面角D-A1C-A的大小(用反三角表示)。
18.(本小题满分12分)
一名学生每天骑自行车上学,途中要经过设红绿灯的4个路口,假设他在每个路口遇到红灯的概率都为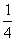 ,且遇到红灯均是相互独立的。
,且遇到红灯均是相互独立的。
(I)求这中学生在途中3次遇到红灯的概率;
(II)求这名学生在途中至少遇到一次红灯的概率;
(III)(只是理科做)设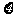 是这名学生上学途中遇到红灯的次数,求
是这名学生上学途中遇到红灯的次数,求
17.(本小题满分10分)
求函数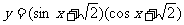 的最大、最小值及其相应的x的集合。
的最大、最小值及其相应的x的集合。
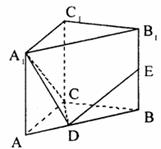
16.在平面几何中△ABC的∠C内角平分线CE分AB所成线段的比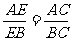 把这个结论类比到空间:在三棱锥A-BCD中(如图)DEC平分二面角A-CD-B且与AB相交于E,则得到类比的结论是
。
把这个结论类比到空间:在三棱锥A-BCD中(如图)DEC平分二面角A-CD-B且与AB相交于E,则得到类比的结论是
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com