
5.函数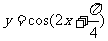 的图象的一条对称轴方程为 ( )
的图象的一条对称轴方程为 ( )
A.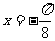 B.
B.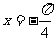 C.
C.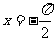 D.
D.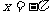
4.若二项式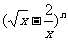 的展开式的第5项为常数项,则n的值为 ( )
的展开式的第5项为常数项,则n的值为 ( )
A.6 B.10 C.12 D.15
3.(理)若复数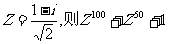 的值为 ( )
的值为 ( )
A.1 B.-1 C. D.
D.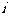
(文)已知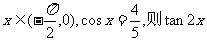 = ( )
= ( )
A.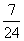 B.-
B.-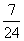 C.
C.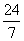 D.-
D.-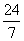
2.抛物线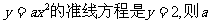 = ( )
= ( )
A.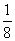 B.
B.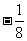 C.8 D.-8
C.8 D.-8
1.若命题“p或q”为真,命题“p且q”为假,则 ( )
A.p、q中至少有一个为真 B.p、q中至少有一个为假
C.p、q中有且只有一个为真 D.p为真,q为假
22.(本小题满分14分)已知函数f(x)=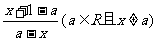
(1)当f(x)的定义域为[a+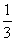 ,a+
,a+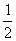 ]时,求f(x)的值域;
]时,求f(x)的值域;
(2)求f(-3a)+f(-2a)+f(-a)+f(0)+f(2a)+f(3a)+f(4a)+f(5a)的值;
(3)设函数g(x)=x2+|(x-a)•f(x)|,求g(x)的最小值.
21.(本小题满分12分)已知双曲线的中心在原点,焦点F1、F2在坐标轴上,离心率为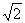 且过点(4,-
且过点(4,-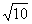 )
)
(1)求双曲线方程;
(2)若点M(3,m)在双曲线上,求证:点M在以F1F2为直径的圆上;
(3)求△F1MF2的面积.
20.(本小题满分12分)设函数f(x)=lnx,g(x)=ax+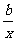 ,函数f(x)的图象与x轴的交点也在函数g(x)的图象上,且在此点有公切线
,函数f(x)的图象与x轴的交点也在函数g(x)的图象上,且在此点有公切线
(1)求a,b的值;
(2)对任意x>0,试比较f(x)与g(x)的大小.
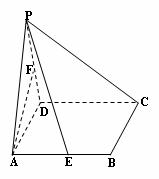
19.(本小题满分12分)已知:四棱锥P-ABCD的底面为正方形,PA⊥底面ABCD,
E、F分别为AB、PD的中点,PA=a,∠PDA=45º
(1)求证:AF∥平面PCE;
(2)求证:平面PCE⊥平面PCD;
(3)求点D到平面PCE的距离.
18.(本小题满分10分)在△ABC中,角A、B、C的对边分别为a,b,c,且cos2C+2cos(A+B)+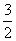 =0
=0
(1)求角C的大小;
(2)若c=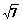 ,a=2,求b的值.
,a=2,求b的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com