
3.等比数列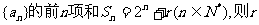 的值为 ( )
的值为 ( )
A.-2 B.-1 C.0 D.1
2.已知实数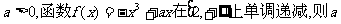 的最大值为 ( )
的最大值为 ( )
A.0 B.4 C.8 D.12
1.设全集I为实数集,集合P,Q满足: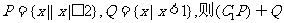 =( )
=( )
A.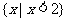 B.
B.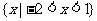 C.
C.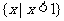 D.
D.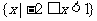
22.(本小题满分14分)
已知点F(4,0),直线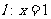 ,动点M在直线l的右侧,以M为圆心的动圆与直线l相切且与以F为圆心半径与它相等的圆外切
,动点M在直线l的右侧,以M为圆心的动圆与直线l相切且与以F为圆心半径与它相等的圆外切
(1)求点M的轨迹方程;
(2)过直线l与x轴的交点P作直线与点M的轨迹交于不同两点M、N,求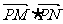 的取值范围;
的取值范围;
(3)在(2)的条件下,设点N关于x轴的对称点为R,问:直线MR是否过定点?若存在,求此定点的坐标,若不存在说明理由。
21.(本小题满分12分)
已知数列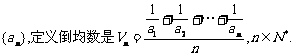
(1)若数列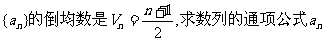
(2)若等比数列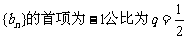 ,其倒均数为Vn,,问是否存在正整数m,使得当
,其倒均数为Vn,,问是否存在正整数m,使得当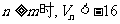 恒成立,若存在,求出m的最小值;若不存在,说明理由。
恒成立,若存在,求出m的最小值;若不存在,说明理由。
20.(本小题满分12分)
已知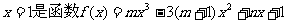 的一个极值点其中
的一个极值点其中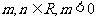
(1)求m与n的关系表达式;
(2)当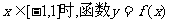 的图象上任意一点的切线斜率恒大于3m,求m的取值范围。
的图象上任意一点的切线斜率恒大于3m,求m的取值范围。
18.(本小题满分12分)
已知圆C: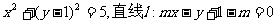 ,
,
(1)求证:对任意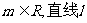 与圆C总有两个交点A,B;
与圆C总有两个交点A,B;
(2)若定点P(1,1)分弦AB为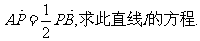
19(本小题满分12分)
在交通拥挤地段,为了确保交通安全,规定机动车相互之间的距离m(米)与车速v(千米/小时)须遵守的关系是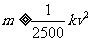 (其中k(米)是车身长,常数),同时规定
(其中k(米)是车身长,常数),同时规定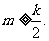
(1)当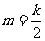 时,求机动车的速度变化范围;
时,求机动车的速度变化范围;
(2)设机动车每小时流量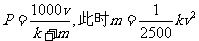 ,应规定怎样的车速,每小时的机动车流量P最大?
,应规定怎样的车速,每小时的机动车流量P最大?
17.(本小题满分12分)
已知函数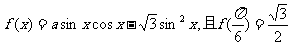 ,
,
(1)求实数a的值;
(2)求函数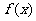 的最小值和单调增区间;
的最小值和单调增区间;
(3)若函数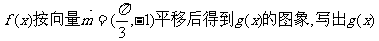 的解析式。
的解析式。
16.已知函数 若
若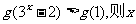 的取值范围是
。
的取值范围是
。
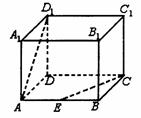
15.如图,正方体ABCD-A1B1C1D1中,E为棱AB的中点,则异面直线AD1与CE所成角的余弦值为 。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com