
1、已知全集U={0,1,2,3,4},集合A={0,1,2},集合B={0,3,4},则(CuA)∩B等于( )
A.{0} B.{3,4} C.{1,2} D.φ
22、(14分)设Sn是正项数列{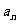 }的前n项和且
}的前n项和且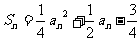 (N∈N+)。
(N∈N+)。
(1)求a1的值; (2)求数列{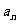 }的通项公式;
}的通项公式;
(3)已知bn=2n,求Tn=a1·b1+a2·b2+a3·b3+…+an·bn
21、(12分)已知直线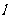 :y=2x-
:y=2x-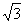 与椭圆C:
与椭圆C: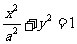 (a>1)交于P、Q两点,以PQ为直径的圆过椭圆C的右顶点A。
(a>1)交于P、Q两点,以PQ为直径的圆过椭圆C的右顶点A。
(1)设PQ中点M(xo ,yo)求证:xo<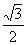 ;
;
(2)求椭圆C的方程
20、(12分)已知函数f(x)=x3+ax-4a3在区间(-|a|,|a|)单调递减。
(1)确定a的取值范围;
(2)求f(1)的取值范围
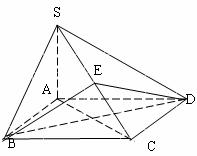
19、(12分)四棱锥S-ABCD的底面是正方形,SA⊥底面ABCD,E是SC上一点。
(1)求证:平面EBD⊥底面SAC。
(2)设SA=4,AB=2,求点A到平面SBD的距离。
18、(12分)某区有四家不同的比萨连锁分店,有3名同学前去就餐(假设每位同学选择某店就餐是等可能的)。
(1)求这3位同学选择在同一连锁分店就餐的概率;
(2)求这3位同学选择在不同三家连锁分店就餐的概率;
(3)求这3位同学中恰有两位同学选择在同一连琐店就餐的概率。
17、(12分)已知向量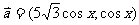 ,
,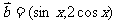 ,函数
,函数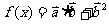 。
。
(1)求函数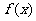 的最小正周期。
的最小正周期。
(2)当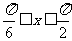 时,求函数
时,求函数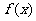 的值域。
的值域。
16、已知以F1(-2,0),F2(2,0)为焦点的椭圆与直线 有且仅有一个交点,则椭圆的长轴长为
。
有且仅有一个交点,则椭圆的长轴长为
。
15、已知直线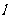 ⊥平面
⊥平面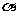 ,直线m
,直线m 平面β,有下列四个命题:
平面β,有下列四个命题:
(1)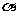 ∥β
∥β
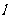 ⊥m; (2)
⊥m; (2)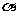 ⊥β
⊥β
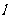 ∥m;
∥m;
(3)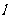 ∥m
∥m
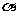 ⊥β; (4)
⊥β; (4)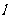 ⊥m
⊥m
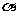 ∥β。
∥β。
其中正确命题的序号 。
14、已知函数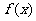 =
=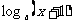 的定义域和值域都是[0,1],则a=
。
的定义域和值域都是[0,1],则a=
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com