
2.下列函数中,反函数是其自身的函数是 ( )
A.y=ex B.y=x2(x≥0) C.y=x3
D.y=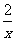
1.设全集U={x|x∈N},A={l,2,4},B={4,6},则A∩CuB是 ( )
A.{1,3} B.{2,4} C.{1,2} D.{1,5}
22.(本小题满分12分)
已知函数F(x)=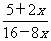 ,设正项数列{ a n}满足a 1=l,
,设正项数列{ a n}满足a 1=l,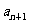 =F (a n).
=F (a n).
(Ⅰ)写出a 2,a 3的值;
(Ⅱ)试比较a n与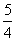 的大小,并说明理由;
的大小,并说明理由;
(Ⅲ)设数列{Bn}满足Bn=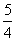 -a n,记Sn=B1+B2+…+Bn,求证:当n≥2时,
-a n,记Sn=B1+B2+…+Bn,求证:当n≥2时,
Sn<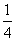 (2n-1).
(2n-1).
21.(本小题满分12分)
设M、N是双曲线上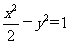 上异于顶点的两个不同的动点,Q为M关于原点的对称点.
上异于顶点的两个不同的动点,Q为M关于原点的对称点.
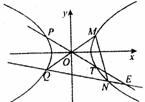
(Ⅰ)求证:若直线MN、NQ的斜率存在,则它们的斜率之积为定值;
(Ⅱ)若P、T分别为M关于y轴、x轴的对称点,且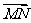 ·
·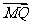 =0,求QN与PT的交点E的轨迹方程.
=0,求QN与PT的交点E的轨迹方程.
20.(本小题满分12分)
已知函数F(x)=ax-(a+1)ln(x+1),其中a>0
(Ⅰ)求F(x)的单调区间;
(Ⅱ)设F(x)的最小值为g(a),求证:-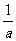 <g (a)<0.
<g (a)<0.
19.(本小题满分12分)
如图直角梯形ABEF中,AB=1,BE=2,AF=3,C为BE的中点,CD∥AB. 沿直线CD将直角梯形ABEF折成直二面角.
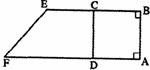
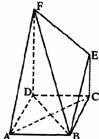
(Ⅰ)求证:AC∥平面BEF;
(Ⅱ)求异面直线BD与EF所成角的大小;
(Ⅲ)求二面角D-BF-E的大小.
18.(本小题满分12分)
某农场在冬季进行一次菌种培养需要5天时间,5天内每天发生低温冻害的概率均为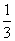 . 如果5天内没有发生冻害,可获利润10万元,有一天发生冻害可获利润5万元,有两天发生冻害可获利润0万元,而发生3天或3天以上冻害则损失2万元.
. 如果5天内没有发生冻害,可获利润10万元,有一天发生冻害可获利润5万元,有两天发生冻害可获利润0万元,而发生3天或3天以上冻害则损失2万元.
(Ⅰ)求一次菌种培养不出现亏损的概率;
(Ⅱ)求一次菌种培养获得利润ξ的分布列和数学期望.
17.(本小题满分10分)
已知A,B,C的坐标分别为A(3,0),B(0,3),C(cosα,sinα),α∈(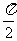 ,
,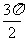 ).
).
(Ⅰ)若|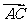 |=|
|=|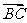 |,求角α的值;
|,求角α的值;
(Ⅱ)若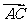 ·
·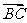 =-1,求
=-1,求 的值.
的值.
16.已知:an=log(n+1)(n+2)(n∈N* ),观察下列运算:
a1·A2=log23·log3 4=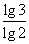 ·
·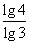 =2,a1·a2·a3·a4·a5·a6=log23·
=2,a1·a2·a3·a4·a5·a6=log23·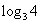
·log45·log56· log67· log78=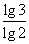 ·
·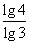 ·…·
·…·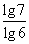 ·
·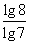 =3.……
=3.……
定义使A1·A2·A3·…Ak为整数的k (k∈N* )叫做企盼数,试确定当A1·A2·A3·…Ak=2008时,企盼数k=______________________.
15.已知直线l,M,平面α、β且l  α,M⊥β有下面四个命题
α,M⊥β有下面四个命题
①α∥β l⊥M ②α⊥β
l⊥M ②α⊥β l∥M ③l∥M
l∥M ③l∥M α⊥β ④l⊥M
α⊥β ④l⊥M α∥β
α∥β
其中正确命题的序号是_______________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com