
1.在下列各数中,与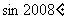 的值最接近的是 ( )
的值最接近的是 ( )
A.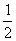 B.
B.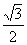 C.-
C.-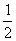 D.-
D.-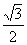
22.(本小题满分12分)
已知f(x)=ax3+bx2+cx在x0处取得极小值-4,使其导函数f '(x)<0的x的范围为(-∞,1)∪(3,+∞).
(Ⅰ)求函数f (x)的解析式;
(Ⅱ)若x∈[2,3 ],求g (x)=f '(x)+6( m-2 )x的最大值.
21.(本小题满分12分)
已知椭圆C的中心在原点,离心率e=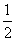 ,且它的一个焦点与抛物线y2=-4x的焦点重合.
,且它的一个焦点与抛物线y2=-4x的焦点重合.
(I)求椭圆C的方程;
(Ⅱ)设F为椭圆C的右焦点,A为左顶点,过F的直线l与椭圆C交于异于A的两点
P、Q,求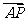 ·
·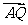 的取值范围.
的取值范围.
20.(本小题满分12分)
如图,面积为6的正方形ABCD所在平面与面积为3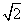 的矩形ABEF所在平面互相垂直,N∈AC,且NC=2AN.设点A在平面CDFE上的射影为M.
的矩形ABEF所在平面互相垂直,N∈AC,且NC=2AN.设点A在平面CDFE上的射影为M.
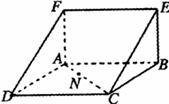
(Ⅰ)求AC与平面CDE所成角的正弦值;
(Ⅱ)证明:MN∥平面ABEF;
(Ⅲ)求点D到平面ACM的距离.
19.(本小题满分12分)
袋子里有大小相同的2个红球和4个黑球,从袋子里随机取球,设取到一个红球得2分,取到一个黑球得1分.
(Ⅰ)若从袋子里随机取出4个球,求得5分的概率;
(Ⅱ)若从袋子里每次摸出一个球,看过颜色后放回,求连续4次摸球共得5分的概率.
18.(本小题满分12分)
已知数列{an}对任意的n∈N*,n≥2,有an=3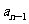 +2,S2=10·
+2,S2=10·
(I)计算a1、a2的值;
(Ⅱ)若数列{Tn}满足Tn=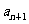 -an,证明{Tn}为等比数列,并求数列{an}的通项公式.
-an,证明{Tn}为等比数列,并求数列{an}的通项公式.
17.(本小题满分l0分)已知△ABC中,a、b、c分别为角A、B、C的对边,A是锐角,且sin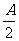 ·cos
·cos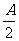 =
=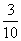 ,
,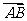 ·
·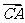 =-8.
=-8.
(I)求bc的值; (Ⅱ)求a的最小值.
16.已知函数f (x)=x3+ax2+bx+c在区间[-l,1]上是减函数,那么a十b的最大值为__________.
15.若(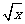 +a)6的展开式中x2项的系数为60,则实数a=_______________.
+a)6的展开式中x2项的系数为60,则实数a=_______________.
14.所有棱长均为3的正三棱柱内接于球O,则球O的表面积为__________________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com