
7.如图,在棱长相等的四面体S-ABC中,E、F分别是SC、AB的中点,则直线EF与SA所成的角为 ( )
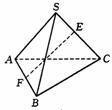
A.90° B.60° C.45° D.30°
6.已知命题p:函数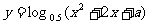 的值域为R,命题q:函数
的值域为R,命题q:函数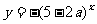 是
是
减函数。若p或q为真命题,p且q为假命题,则实数a的取值范围是 ( )
A.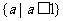 B.
B.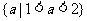
C. D.
D.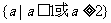
5.已知 ,则
,则 的值是 ( )
的值是 ( )
A. B.
B.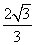 C.
C. D.
D.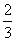
4.若等差数列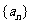 的前5项之和
的前5项之和 ,且
,且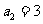 ,则
,则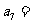 ( )
( )
A.12 B.13 C.14 D.15
3.已知图1是函数 的图象,则图2中的图象对应的函数可能是 ( )
的图象,则图2中的图象对应的函数可能是 ( )
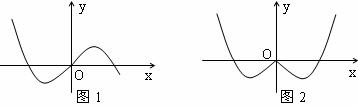
A.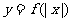 B.
B.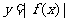
C.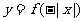 D.
D.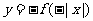
2.已知条件p: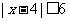 ;条件q:
;条件q: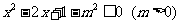 ,若p是q的充分不必要条件,则m的取值范围是 ( )
,若p是q的充分不必要条件,则m的取值范围是 ( )
A.[21,+∞] B.[9,+∞] C.[19,+∞] D.(0,+∞)
1.若复数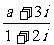 (
(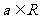 ,
, 为虚数单位)是纯虚数,则实数
为虚数单位)是纯虚数,则实数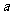 的值为 ( )
的值为 ( )
A.-6 B.13 C.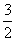 D.
D.
22.(本小题满分12分)已知函数 当
当 时,总有
时,总有 .
.
(I)求函数f(x)的解析式;
(II)设函数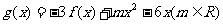 ,求证:当
,求证:当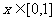 时,若
时,若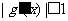 恒成立,则|g(x)|≤3.5也恒成立.
恒成立,则|g(x)|≤3.5也恒成立.
21.(本小题满分12分) 定义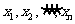 的“倒平均数”为
的“倒平均数”为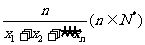 ,已知数列
,已知数列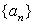 前
前 项的“倒平均数”为
项的“倒平均数”为 .
.
(I)记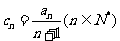 ,试比较
,试比较 与
与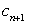 的大小;
的大小;
(II)是否存在实数 ,使得当
,使得当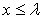 时,
时,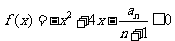 对任意
对任意 恒成立?若存在,求出最大的实数
恒成立?若存在,求出最大的实数 ;若不存在,说明理由.
;若不存在,说明理由.
20.(本小题满分12分)设数列 的前
的前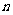 项和为
项和为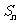 ,如果
,如果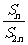 为常数,则称数列
为常数,则称数列 为“科比数列”.
为“科比数列”.
(Ⅰ)已知等差数列 的首项为1,公差不为零,若
的首项为1,公差不为零,若 为“科比数列”,求
为“科比数列”,求 的通项公式;
的通项公式;
(Ⅱ)设数列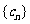 的各项都是正数,前
的各项都是正数,前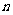 项和为
项和为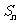 ,若
,若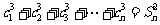 对任意
对任意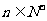 都成立,试推断数列
都成立,试推断数列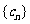 是否为“科比数列”?并说明理由.
是否为“科比数列”?并说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com