
15.[2009年上海市普通高等学校春季招生考试20.]设函数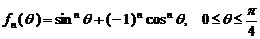 ,其中
,其中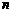 为正整数.
为正整数.
(1)判断函数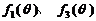 的单调性,并就
的单调性,并就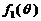 的情形证明你的结论;
的情形证明你的结论;
(2)证明: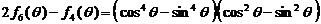 ;
;
(3)对于任意给定的正整数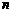 ,求函数
,求函数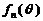 的最大值和最小值.
的最大值和最小值.
[解析](1)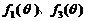 在
在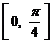 上均为单调递增的函数.
…… 2分
上均为单调递增的函数.
…… 2分
对于函数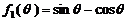 ,设
,设 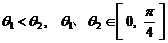 ,则
,则
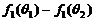
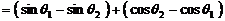 ,
,
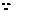
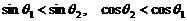 ,
,
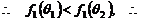 函数
函数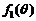 在
在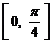 上单调递增.
…… 4分
上单调递增.
…… 4分
(2)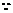 原式左边
原式左边
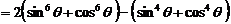
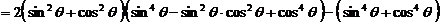
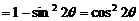 .
…… 6分
.
…… 6分
又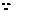 原式右边
原式右边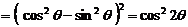 .
.
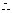
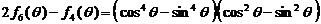 .
…… 8分
.
…… 8分
(3)当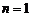 时,函数
时,函数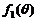 在
在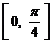 上单调递增,
上单调递增,
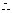
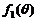 的最大值为
的最大值为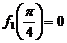 ,最小值为
,最小值为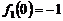 .
.
当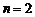 时,
时,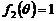 ,
,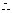 函数
函数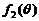 的最大、最小值均为1.
的最大、最小值均为1.
当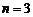 时,函数
时,函数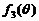 在
在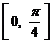 上为单调递增.
上为单调递增.
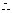
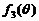 的最大值为
的最大值为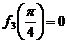 ,最小值为
,最小值为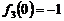 .
.
当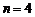 时,函数
时,函数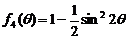 在
在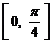 上单调递减,
上单调递减,
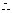
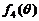 的最大值为
的最大值为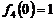 ,最小值为
,最小值为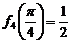 .
…… 11分
.
…… 11分
下面讨论正整数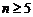 的情形:
的情形:
当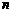 为奇数时,对任意
为奇数时,对任意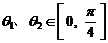 且
且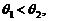
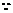
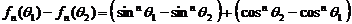 ,
,
以及 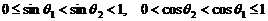 ,
,
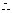
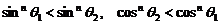 ,从而
,从而 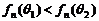 .
.
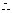
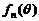 在
在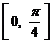 上为单调递增,则
上为单调递增,则
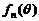 的最大值为
的最大值为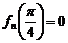 ,最小值为
,最小值为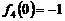 .
…… 14分
.
…… 14分
当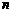 为偶数时,一方面有
为偶数时,一方面有 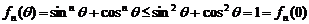 .
.
另一方面,由于对任意正整数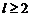 ,有
,有
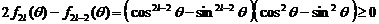 ,
,
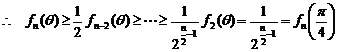 .
.
 函数
函数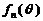 的最大值为
的最大值为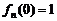 ,最小值为
,最小值为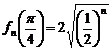 .
.
综上所述,当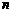 为奇数时,函数
为奇数时,函数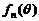 的最大值为
的最大值为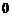 ,最小值为
,最小值为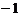 .
.
当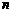 为偶数时,函数
为偶数时,函数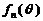 的最大值为
的最大值为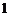 ,最小值为
,最小值为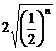 .
…… 18分
.
…… 18分
12.[安徽省示范高中皖北协作区2009年高三联考(理)22](本小题14分)设函数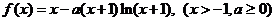
(Ⅰ)求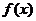 的单调区间;
的单调区间;
(Ⅱ)当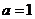 时,若方程
时,若方程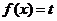 在
在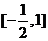 上有两个实数解,求实数t的取值范围;
上有两个实数解,求实数t的取值范围;
(Ⅲ)证明:当m>n>0时,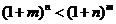 。
。
[解析]:22、(Ⅰ)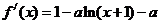
①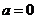 时,
时,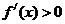 ∴
∴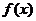 在(-1,+
在(-1,+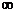 )上市增函数
)上市增函数
②当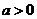 时,
时,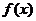 在
在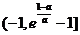 上递增,在
上递增,在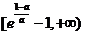 单调递减
单调递减
(Ⅱ)由(Ⅰ)知,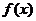 在
在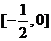 上单调递增,在
上单调递增,在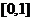 上单调递减
上单调递减
又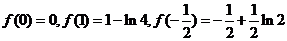 ∴
∴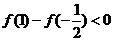
∴当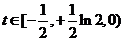 时,方程
时,方程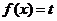 有两解
有两解
(Ⅲ)要证: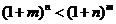 只需证
只需证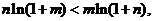
只需证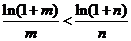
设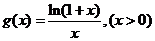 , 则
, 则
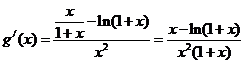
由(Ⅰ)知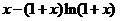 在
在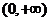 单调递减
单调递减
∴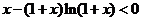 ,即
,即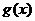 是减函数,而m>n
是减函数,而m>n
∴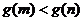 ,故原不等式成立。
,故原不等式成立。
10.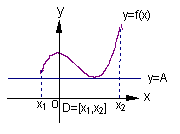 [东北育才学校2009届高三第三次模拟考试(理)24.]如右图(1)所示,定义在区间
[东北育才学校2009届高三第三次模拟考试(理)24.]如右图(1)所示,定义在区间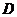 上的函数
上的函数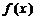 ,如果满足:对
,如果满足:对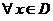 ,
,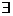 常数A,都有
常数A,都有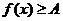 成立,则称函数
成立,则称函数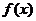 在区间
在区间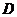 上有下界,其中
上有下界,其中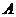 称为函数的下界. (提示:图(1)、(2)中的常数
称为函数的下界. (提示:图(1)、(2)中的常数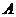 、
、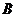 可以是正数,也可以是负数或零)
可以是正数,也可以是负数或零)
(Ⅰ)试判断函数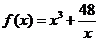 在
在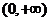 上是否有下界?并说明理由;
上是否有下界?并说明理由;
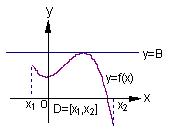 (Ⅱ)又如具有右图(2)特征的函数称为在区间
(Ⅱ)又如具有右图(2)特征的函数称为在区间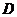 上有上界.
上有上界.
请你类比函数有下界的定义,给出函数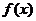 在区间
在区间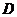 上有上界的定义,并判断(Ⅰ)中的函数在
上有上界的定义,并判断(Ⅰ)中的函数在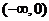 上是否有上界?并说明理由;
上是否有上界?并说明理由;
(Ⅲ)若函数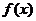 在区间
在区间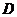 上既有上界又有下界,则称函数
上既有上界又有下界,则称函数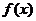 在区间
在区间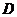 上有界,函数
上有界,函数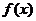 叫做有界函数.试探究函数
叫做有界函数.试探究函数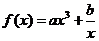 (
(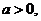
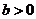
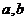 是常数)是否是
是常数)是否是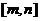 (
(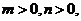
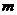 、
、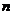 是常数)上的有界函数?
是常数)上的有界函数?
[解析]:24.(I)解法1:∵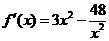 ,由
,由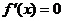 得
得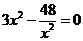 ,
,
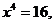 ∵
∵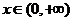 , ∴
, ∴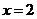 ,-----------------2分
,-----------------2分
∵当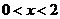 时,
时,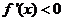 ,∴函数
,∴函数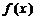 在(0,2)上是减函数;
在(0,2)上是减函数;
当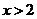 时,
时,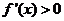 ,∴函数
,∴函数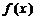 在(2,+
在(2,+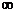 )上是增函数;
)上是增函数;
∴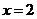 是函数的在区间(0,+
是函数的在区间(0,+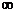 )上的最小值点,
)上的最小值点,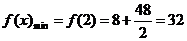
∴对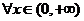 ,都有
,都有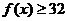 ,------------------------------------4分
,------------------------------------4分
即在区间(0,+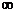 )上存在常数A=32,使得对
)上存在常数A=32,使得对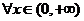 都有
都有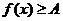 成立,
成立,
∴函数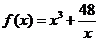 在(0,+
在(0,+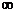 )上有下界. ---------------------5分
)上有下界. ---------------------5分
[解法2: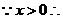
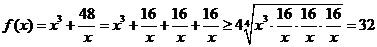
当且仅当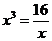 即
即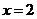 时“=”成立
时“=”成立
∴对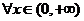 ,都有
,都有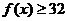 ,
,
即在区间(0,+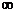 )上存在常数A=32,使得对
)上存在常数A=32,使得对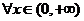 都有
都有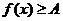 成立,
成立,
∴函数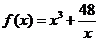 在(0,+
在(0,+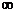 )上有下界.]
)上有下界.]
(II)类比函数有下界的定义,函数有上界可以这样定义:
定义在D上的函数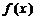 ,如果满足:对
,如果满足:对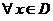 ,
,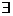 常数B,都有
常数B,都有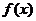 ≤B成立,则称函数
≤B成立,则称函数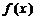 在D上有上界,其中B称为函数的上界. -----7分
在D上有上界,其中B称为函数的上界. -----7分
设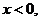
 则
则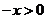 ,由(1)知,对
,由(1)知,对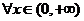 ,都有
,都有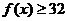 ,
,
∴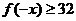 ,∵函数
,∵函数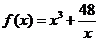 为奇函数,∴
为奇函数,∴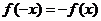
∴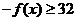 ,∴
,∴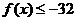
即存在常数B=-32,对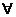
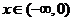 ,都有
,都有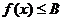 ,
,
∴函数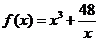 在(-
在(-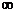 , 0)上有上界. ---------9分
, 0)上有上界. ---------9分
(III)∵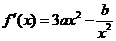 ,
,
由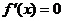 得
得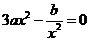 ,∵
,∵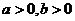

∴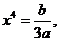 ∵
∵ 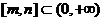 , ∴
, ∴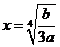 ,----------10分
,----------10分
∵当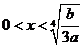 时,
时,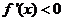 ,∴函数
,∴函数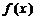 在(0,
在(0,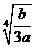 )上是减函数;
)上是减函数;
当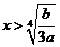 时,
时,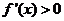 ,∴函数
,∴函数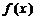 在(
在(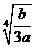 ,+
,+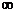 )上是增函数;
)上是增函数;
∴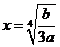 是函数的在区间(0,+
是函数的在区间(0,+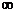 )上的最小值点,
)上的最小值点,
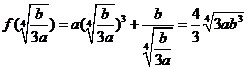 ---------------------11分
---------------------11分
①当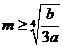 时,函数
时,函数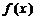 在
在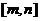 上是增函数;
上是增函数;
∴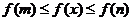
∵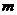 、
、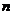 是常数,∴
是常数,∴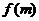 、
、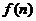 都是常数
都是常数
令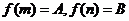 ,
,
∴对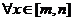 ,
,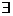 常数A,B,都有
常数A,B,都有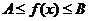
即函数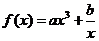 在
在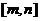 上既有上界又有下界-------------------------12分
上既有上界又有下界-------------------------12分
②当 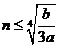 时函数
时函数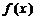 在
在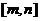 上是减函数
上是减函数
∴对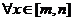 都有
都有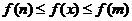
∴函数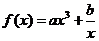 在
在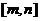 上有界.-------------------------13分
上有界.-------------------------13分
③当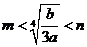 时,函数
时,函数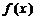 在
在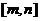 上有最小值
上有最小值
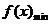 =
=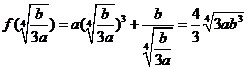
令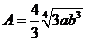 ,令B=
,令B=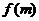 、
、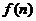 中的最大者
中的最大者
则对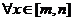 ,
,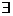 常数A,B,都有
常数A,B,都有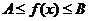
∴函数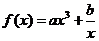 在
在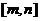 上有界.
上有界.
综上可知函数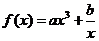 是
是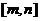 上的有界函数--------------14分
上的有界函数--------------14分
9.[东北育才学校2009届高三第三次模拟考试(文)22.] (本小题满分14分)设等比数列{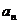 }的前
}的前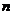 项和
项和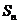 ,首项
,首项 ,公比
,公比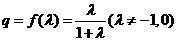 .
.
(Ⅰ)证明: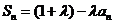 ;
;
(Ⅱ)若数列{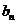 }满足
}满足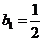 ,
,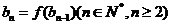 ,求数列{
,求数列{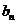 }的通项公式;
}的通项公式;
(Ⅲ)若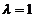 ,记
,记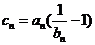 ,数列{
,数列{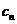 }的前项和为
}的前项和为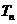 ,求证:当
,求证:当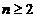 时,
时,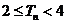 .
.
[解析]:(Ⅰ)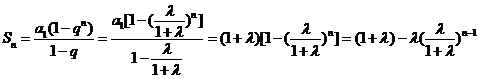 ……2分
……2分
而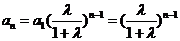 ……………………………………………3分
……………………………………………3分
所以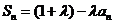 …………………………………………4分
…………………………………………4分
(Ⅱ)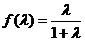 ,
,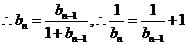 ,
……………………………6分
,
……………………………6分
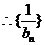 是首项为
是首项为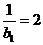 ,公差为1的等差数列,
,公差为1的等差数列,
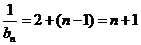 ,即
,即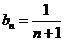 .
………………………………8分
.
………………………………8分
(Ⅲ) 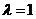 时,
时, 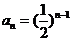 ,
, 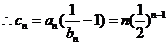 …………………………9分
…………………………9分
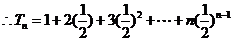
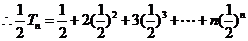
相减得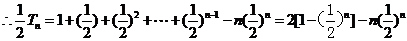
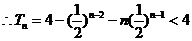 ,
…………………………12分
,
…………………………12分
又因为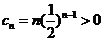 ,
,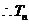 单调递增,
单调递增, 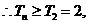
故当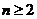 时,
时, 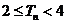 .
……………………………………………………14分
.
……………………………………………………14分
7.[河北省石家庄市2009年高中毕业班复习教学质量检测(一)22.](本题满分12分)[理科]已知函数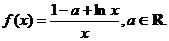
(I)求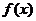 的极值;
的极值;
(II)若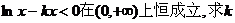 的取值范围;
的取值范围;
(III)已知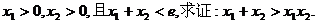
[解析]:(Ⅰ)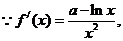 令
令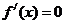 得
得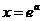 ……………2分
……………2分
当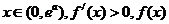 为增函数;
为增函数;
当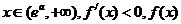 为减函数,
为减函数,
可知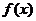 有极大值为
有极大值为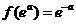 …………………………..4分
…………………………..4分
(Ⅱ)欲使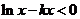 在
在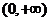 上恒成立,只需
上恒成立,只需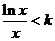 在
在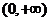 上恒成立,
上恒成立,
设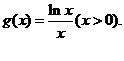
 由(Ⅰ)知,
由(Ⅰ)知,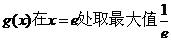 ,
,
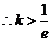 ……………………8分
……………………8分
(Ⅲ)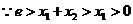 ,由上可知
,由上可知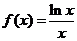 在
在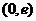 上单调递增,
上单调递增,
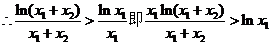 ①,
①,
同理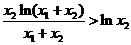 ②…………………………..10分
②…………………………..10分
两式相加得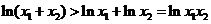
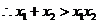 ……………………………………12分
……………………………………12分
6.[河南省普通高中2009年高中毕业班教学质量调研考试(理)22.](本小题满分12分)
已知数列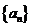 满足
满足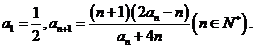
(1)求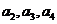 ;
;
(2)已知存在实数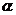 ,使
,使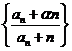 为公差为
为公差为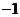 的等差数列,求
的等差数列,求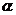 的值;
的值;
(3)记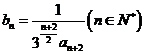 ,数列
,数列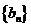 的前
的前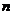 项和为
项和为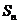 ,求证:
,求证: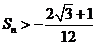 .
.
[解析]:22.解:(1)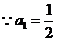 ,由数列
,由数列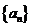 的递推公式得
的递推公式得
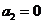 ,
,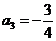 ,
,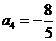 .……………………………………………………3分
.……………………………………………………3分
(2)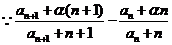
=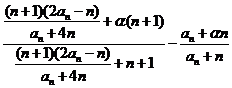
=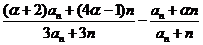 =
=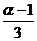 .……………………5分
.……………………5分
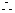 数列
数列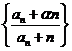 为公差是
为公差是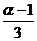 的等差数列.
的等差数列.
由题意,令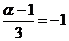 ,得
,得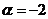 .……………………7分
.……………………7分
(3)由(2)知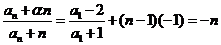 ,
,
所以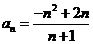 .……………………8分
.……………………8分
此时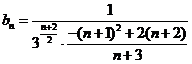 =
=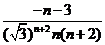
=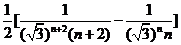 ,……………………10分
,……………………10分
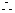
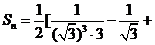
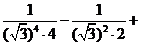
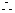
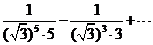
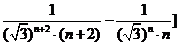 =
=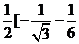
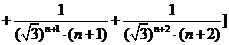
>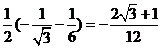 .……………………12分
.……………………12分
4. [湖北省2009届高三八校联考第二次(理)21.](本小题满分14分)已知数列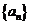 中,
中,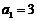 ,
,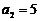 ,其前
,其前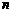 项和
项和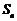 满足
满足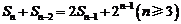 .令
.令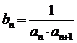 .
.
(Ⅰ)求数列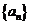 的通项公式;
的通项公式;
(Ⅱ)若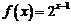 ,求证:
,求证: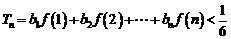 (
(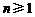 );
);
(Ⅲ)令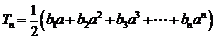 (
(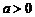 ),求同时满足下列两个条件的所有
),求同时满足下列两个条件的所有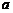 的值:①对于任意正整数
的值:①对于任意正整数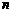 ,都有
,都有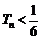 ;②对于任意的
;②对于任意的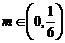 ,均存在
,均存在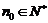 ,使得
,使得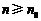 时,
时,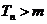 .
.
[解](Ⅰ)由题意知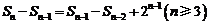 即
即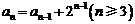 ……1′
……1′
∴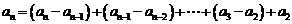
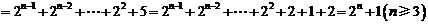 ……2′
……2′
检验知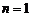 、
、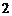 时,结论也成立,故
时,结论也成立,故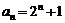 .…………3′
.…………3′
(Ⅱ)由于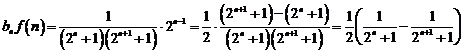
故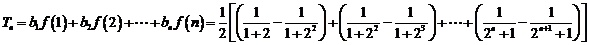
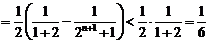 .…………6′
.…………6′
(Ⅲ)(ⅰ)当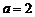 时,由(Ⅱ)知:
时,由(Ⅱ)知: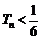 ,即条件①满足;又
,即条件①满足;又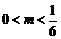 ,
,
∴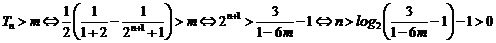 .
.
取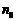 等于不超过
等于不超过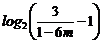 的最大整数,则当
的最大整数,则当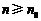 时,
时,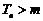 .…9′
.…9′
(ⅱ)当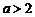 时,∵
时,∵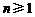 ,
,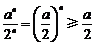 ,∴
,∴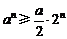 ,∴
,∴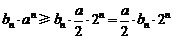 .
.
∴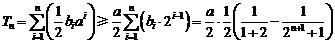 .
.
由(ⅰ)知存在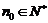 ,当
,当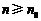 时,
时,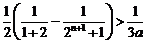 ,
,
故存在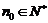 ,当
,当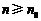 时,
时,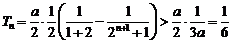 ,不满足条件. …12′
,不满足条件. …12′
(ⅲ)当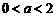 时,∵
时,∵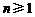 ,
,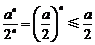 ,∴
,∴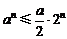 ,∴
,∴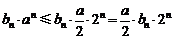 .
.
∴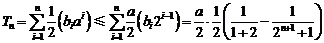 .
.
取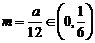 ,若存在
,若存在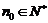 ,当
,当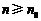 时,
时,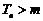 ,则
,则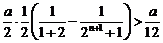 .
.
∴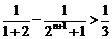 矛盾. 故不存在
矛盾. 故不存在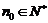 ,当
,当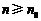 时,
时,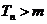 .不满足条件.
.不满足条件.
综上所述:只有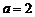 时满足条件,故
时满足条件,故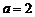 .…………14′
.…………14′
2.[江苏省姜堰中学高三数学阶段调研试卷](本小题满分16分)函数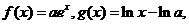 其中
其中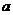 为常数,且函数
为常数,且函数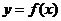 和
和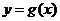 的图像在其与坐标轴的交点处的切线互相平行
的图像在其与坐标轴的交点处的切线互相平行
(1)、求函数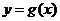 的解析式
的解析式
(2)、若关于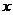 的不等式
的不等式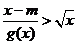 恒成立,求实数
恒成立,求实数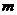 的取值范围。
的取值范围。
[解析]:(1)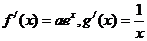 ------2
------2
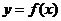 的图像与坐标轴的交点为
的图像与坐标轴的交点为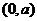 ,
,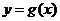 的图像与坐标轴的交点为
的图像与坐标轴的交点为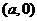
由题意得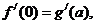 即
即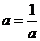 ,
------3
,
------3
又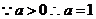
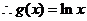 ------4
------4
(2)由题意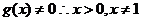
当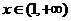 时,
时,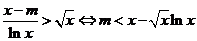 -------6
-------6
令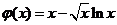
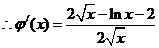 ------7
------7
令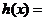
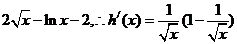 ------9
------9
当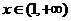 时,
时,
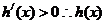 单调递增。
单调递增。
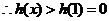 ------10
------10
由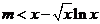 在
在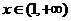 上恒成立,
上恒成立,
得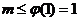 ------12
------12
当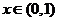 时,
时,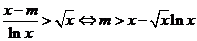 ------13
------13
可得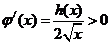
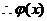 单调递增。------14
单调递增。------14
由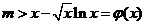 在
在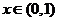 上恒成立,得
上恒成立,得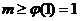 ------15
------15
综上,可知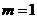 ------16
------16
22. (14分)某无色溶液X,由Na+、Ag+、Ba2+、Al3+、Fe3+、AlO2-、CO32-、SO42-中的若干种离子组成,取该溶液进行如下实验:
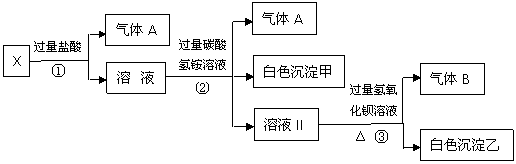 (1)气体A的成分是
(填化学式,下同),气体B的成分是 。
(1)气体A的成分是
(填化学式,下同),气体B的成分是 。
(2)写出步骤①发生反应的所有离子方程式 。
(3)写出步骤②形成白色沉淀甲的离子方程式 。
(4)通过上述实验,可确定X溶液中一定存在的离子是 ,
尚未确定是否存在的离子是 ,只要设计一个简单的后续实验就可以确
定该离子是否存在,该方法是 。
21. (12分)硫酸亚铁晶体(FeSO4·7H2O)在医药上作补血剂。某课外小组测定该补血剂中铁元素的含量。实验步骤如下:
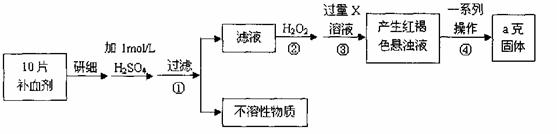 请回答下列问题:
请回答下列问题:
(1)步骤②加入过量H2O2的目的:
(2)步骤③中反应的离子方程式:
(3)步骤④中一系列处理的操作步骤:过滤、 、灼烧、 、称量。
(4)若实验无损耗,则每片补血剂含铁元素的质量 g(用含a的代数式表示)。
(5)该小组有些同学认为用KMnO4溶液滴定也能进行铁元素含量的测定。
(5Fe2++MnO4-+8H+ = 5Fe3++Mn2++4H2O)
①实验前,首先要精确配制一定物质的量浓度的KMnO4溶液250mL,配制时需要的仪器除天平、玻璃棒、烧杯、胶头滴管外,还需
②上述实验中的KMnO4溶液需要酸化,用于酸化的酸是 。
a.稀硝酸 b.稀硫酸 c.稀盐酸 d.浓硝酸
③某同学设计的下列滴定方式中,最合理的是 (夹持部分略去)(填字母序号)
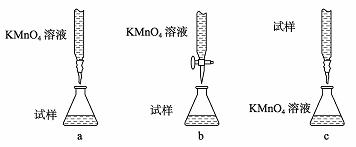
(6)正常人每天应补充14mg左右的铁。其中绝大部分来自于食物。如果全部通过服用含FeSO4·7H2O的片剂来补充铁,则正常人每天服需用含 mg
FeSO4·7H2O的片剂。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com