
2.正态曲线及其性质
对于正态分布函数:
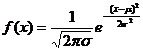 ,x∈(-∞,+∞)
,x∈(-∞,+∞)
由于中学知识范围的限制,不必去深究它的来龙去脉,但对其函数图像即正态曲线可通过描点(或计算机中的绘图工具)画出课本图1-4中的图(1)、(2)、(3),由此,我们不难自己总结出正态曲线的性质。
1.正态分布的重要性
正态分布是概率统计中最重要的一种分布,其重要性我们可以从以下两方面来理解:一方面,正态分布是自然界最常见的一种分布。一般说来,若影响某一数量指标的随机因素很多,而每个因素所起的作用都不太大,则这个指标服从正态分布。例如,产品尺寸是一类典型的总体,对于成批生产的产品,如果生产条件正常并稳定,即工艺、设备、技术、操作、原料、环境等可以控制的条件都相对稳定,而且不存在产生系统误差的明显因素,那么,产品尺寸的总体分布就服从正态分布。又如测量的误差;炮弹落点的分布;人的生理特征的量:身高、体重等;农作物的收获量等等,都服从或近似服从正态分布。另一方面,正态分布具有许多良好的性质,很多分布可以用正态分布来近似描述,另外,一些分布又可以通过正态分布来导出,因此在理论研究中正态分布也十分重要。
3.分层抽样:当已知总体由差异明显的几部分组成时,常将总体分成几部分,然后按照各部分所占的比进行抽样,这种抽样叫做分层抽样,其中所分成的各部分叫做层。
㈤总体分布的估计
总体分布:总体取值的概率分布规律通常称为总体分布。
总体密度曲线:当样本容量无限增大,分组的组距无限缩小,那么频率分布直方图就会无限接近于一条光滑曲线,即总体密度曲线。
㈥正态分布
正态分布:如果总体密度曲线是以下函数的图象:
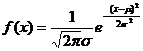 ,
,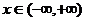 ①
①
式中的实数μ、σ(σ>0)是参数,分别表示总体的平均数与标准差,这个总体是有无限容量的抽象总体。其分布叫做正态分布,常记作N(μ,σ2)。①的图象被称为正态曲线。
特别地,在函数①中,当μ=0,σ=1时,正态总体称为标准正态总体,这时,相应的函数
表达式是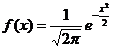 ,
,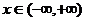 , ②
, ②
相应的曲线称为标准正态曲线。
当我们不知道一个总体的分布时,往往总是从总体中抽取一个样本,并用样本的频率分布去估计总体的分布,而且随着样本容量越大分组的组距越小,样本的频率分布就更加接近总体分布。当样本容量无限增大且分组的组距无限缩小时,频率分布直方图就会演变成一条光滑曲线,即反映总体分布的总体密度曲线。可以知道,反映总体分布的总体密度曲线的形状是形形色色的,不同形状的总体密度曲线是不同总体分布的反映,而正态分布以及反映这种分布的正态曲线是异彩纷呈的总体分布及总体密度曲线中的一类重要分布。
2.系统抽样:当总体中的个数较多时,可将总体分成均衡的几个部分,然后按照预先定出的规则,从每一部分抽取1个个体,得到所需要的样本,这种抽样叫做系统抽样(也称为机械抽样)。
系统抽样的步骤可概括为:(1)将总体中的个体编号;(2)将整个的编号进行分段;(3)确定起始的个体编号;(4)抽取样本。
1.简单随机抽样:设一个总体的个数为N。如果通过逐个抽取的方法从中抽取一个样本,且每次抽取时各个个体被抽到的概率相等,就称这样的抽样为简单随机抽样。实现简单随机抽样,常用抽签法和随机数表法。
4.二项分布的期望与方差
若 -B (n,p),则E
-B (n,p),则E =np,D
=np,D =np (1-p)。
=np (1-p)。
㈣抽样方法
三种常用抽样方法:
3.离散型随机变量期望和方差的性质
E (a +b)=aE
+b)=aE +b,D (a
+b,D (a +b)=a2 D
+b)=a2 D 。
。
2.离散型随机变量期望和方差的计算公式
设离散型随机变量 的分布列为P(
的分布列为P( =xi)=pi,i=1,2,…,则:
=xi)=pi,i=1,2,…,则:
E =
= i pi,D
i pi,D =
=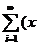 i-E
i-E )2 pi=
)2 pi= i2 pi-(E
i2 pi-(E )2=E(
)2=E( 2)-(E
2)-(E )2。
)2。
1.在实际问题中,人们常关心随机变量的特征,而不是随机变量的具体值。离散型随机变量的期望和方差都是随机变量的特征数,期望反映了随机变量的平均取值,方差与标准差都反映了随机变量取值的稳定与波动、集中与离散的程度。其中标准差与随机变量本身有相同的单位。
6.线性回归:
当变量x取值一定时,如果相应的变量y的取值带有一定的随机性,那么就说变量y与x具有相关关系。对于它们的一组观测值来说,如果与之相应的在平面直角坐标系中的点大体上集中在一条直线的附近,就说变量y与x之间具有线性相关关系。
相关系数用来检验线性相关显著水平,通常通过查表取显著水平0.05自由度n-2的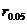 ,若
,若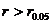 为显著;否则为不显著。
为显著;否则为不显著。
㈢离散型随机变量的分布列
随机变量:如果随机试验的结果可以用一个变量来表示,那么这样的变量叫做随机变量。随机变量最常见的两种类型,即离散型随机变量和连续型随机变量。如果对于随机变量可能取的值,可以按一定次序一一列出,这样的随机变量叫做离散型随机变量;如果随机变量可以取某一区间内的一切值,这样的随机变量叫做连续型随机变量。
离散型随机变量的分布列:如果离散型随机变量 的可能取值为xi(i=1,2,…),由于试验的各个结果的出现有一定的概率,于是随机变量
的可能取值为xi(i=1,2,…),由于试验的各个结果的出现有一定的概率,于是随机变量 取每一个值也有一定的概率P(
取每一个值也有一定的概率P( =xi)=pi,人们常常习惯地把它们写成表格的形式,如:
=xi)=pi,人们常常习惯地把它们写成表格的形式,如:
 |
x1 |
x2 |
… |
xi |
… |
|
P |
p1 |
p2 |
… |
pi |
… |
这种表即为随机变量 的概率分布,简称为
的概率分布,简称为 的分布列。
的分布列。
分布列的表达式可有如下几种:(1)表格形式;(2)一组等式;(3)压缩为一个带“i”的等式。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com